题目内容
已知函数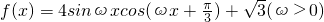 的最小正周期为π.
的最小正周期为π.
(1)求f(x)的解析式;
(2)求f(x)在区间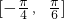 上的最大值和最小值及取得最值时x的值.
上的最大值和最小值及取得最值时x的值.
解:(1)∵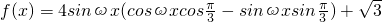 ,------(1分)
,------(1分)
=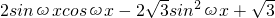 =
=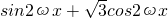 ---(3分)
---(3分)
=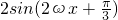 .--------(4分)
.--------(4分)
∵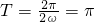 ,∴ω=1,----(5分)
,∴ω=1,----(5分)
∴ .------(6分)
.------(6分)
(2)∵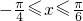 ,∴
,∴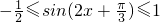 ,即-1≤f(x)≤2,--------(9分)
,即-1≤f(x)≤2,--------(9分)
当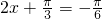 ,即
,即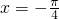 时,f(x)min=-1,
时,f(x)min=-1,
当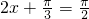 ,即
,即 时,f(x)max=2.-----(12分)
时,f(x)max=2.-----(12分)
分析:(1)利用两角和差的正弦公式化简函数f(x)的解析式为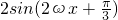 ,再根据最小正周期为π求得ω的值,即可进一步确定函数的解析式.
,再根据最小正周期为π求得ω的值,即可进一步确定函数的解析式.
(2)根据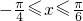 ,利用正弦函数的定义域和值域求得f(x)在区间
,利用正弦函数的定义域和值域求得f(x)在区间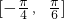 上的最大值和最小值,及取得最值时x的值.
上的最大值和最小值,及取得最值时x的值.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,两角和差的正弦公式,正弦函数的定义域和值域,属于中档题.
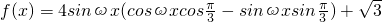 ,------(1分)
,------(1分)=
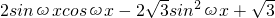 =
=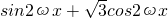 ---(3分)
---(3分)=
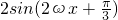 .--------(4分)
.--------(4分)∵
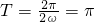 ,∴ω=1,----(5分)
,∴ω=1,----(5分)∴
 .------(6分)
.------(6分)(2)∵
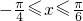 ,∴
,∴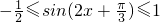 ,即-1≤f(x)≤2,--------(9分)
,即-1≤f(x)≤2,--------(9分)当
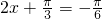 ,即
,即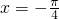 时,f(x)min=-1,
时,f(x)min=-1,当
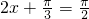 ,即
,即 时,f(x)max=2.-----(12分)
时,f(x)max=2.-----(12分)分析:(1)利用两角和差的正弦公式化简函数f(x)的解析式为
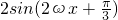 ,再根据最小正周期为π求得ω的值,即可进一步确定函数的解析式.
,再根据最小正周期为π求得ω的值,即可进一步确定函数的解析式.(2)根据
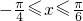 ,利用正弦函数的定义域和值域求得f(x)在区间
,利用正弦函数的定义域和值域求得f(x)在区间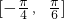 上的最大值和最小值,及取得最值时x的值.
上的最大值和最小值,及取得最值时x的值.点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,两角和差的正弦公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
. 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.