Question

已知直线x+2y+m=0(m∈R)与抛物线C：y²=x相交于不同的两点A，B，

（1）求实数m的取值范围；

（2）在抛物线C上是否存在一个定点P，对（1）中任意的m的值，都有直线PA与PB互为相反数？若存在，求出点P的坐标；若不存在，试说明理由.

Answer 1

解析：(1)∵抛物线与直线有两个不同的交点，

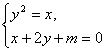∵有两个不同的解，

即方程y²+2y+m=0有两个不同的解，

∴Δ=4-4m＞0,即m＜1.

(2)设A（y₁²,y₁）,(y₂²,y₂),P(y₀²,y₀),

由k_AB=,得y₁+y₂=-2,

k_PA=,

k_PB=，

假设在抛物线上存在定点P使得直线PA与PB的斜率互为相反数，即：,

即：2y₀=-(y₁+y₂)=2,得y₀=1.

∴存在定点P（1，1）使得直线PA与PB的斜率互为相反数.