题目内容
在正四棱柱ABCD—A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的任一点.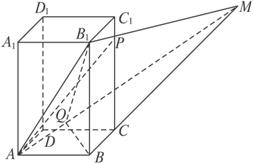
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成二面角的余弦值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?
解法一:(1)证明:由题意可知,不论P点在棱CC1上的任何位置,AP在底面ABCD内射影都是AC,∵BD⊥AC,

∴BD⊥AP.
(2)延长B1P和BC,设B1P∩BC=M,连结AM,则AM=平面AB1P∩平面ABCD,过B作BQ⊥AM于Q,连结B1Q,由于BQ是B1Q在底面ABCD内的射影,所以B1Q⊥AM,故∠B1QB就是所求二面角的平面角.
依题意,知CM=2B1C1,从而BM=3BC.
∴AM=![]() BC.在Rt△ABM中,
BC.在Rt△ABM中,
BQ=![]() .在Rt△B1BQ中,tan∠B1QB=
.在Rt△B1BQ中,tan∠B1QB= .
.
∴tan∠B1QB![]() .∴1+tan2∠B1QB=
.∴1+tan2∠B1QB=![]() .∴1+
.∴1+![]() .∴cos∠B1QB=
.∴cos∠B1QB=![]() 为所求.
为所求.
(3)设CP=a,BC=m,则BB1=2m,C1P=2m-a,从而B1P2=m2+(2m-3)2,AB12=m2+4m2=5m2,AC=![]() m.在Rt△ACP中,cos∠APC=
m.在Rt△ACP中,cos∠APC=![]() .在△PAB1中,cos∠PAB1=
.在△PAB1中,cos∠PAB1=![]() .依题意,得∠PAC=∠PAB1.
.依题意,得∠PAC=∠PAB1.
∴![]() .
.
∴AP2+AB12-B1P2=2AC·AB1,
即a2+2m2+5m2-[m2+(2m-a)2]=2![]() m·
m·![]() m.
m.
∴a=![]() m=
m=![]() BB1.故P距C点的距离是侧棱的
BB1.故P距C点的距离是侧棱的![]() .
.
解法二:(1)证明:如图,建立空间直角坐标系.设CP=a,CC1=6,∴B1(0,3,6),B(0,3,0),C(-3,3,0),D(-3,0,0),P(-3,3,a).![]() =(-3,3,a),
=(-3,3,a),![]() =(0,3,6),
=(0,3,6),![]() =(-3,-3,0),∵
=(-3,-3,0),∵![]() ·
·![]() =0,∴
=0,∴![]() ⊥
⊥![]() .∴BD⊥AP.
.∴BD⊥AP.

(2)设n⊥平面AB1P,n=(x,y,z),∵CC1=3C1P,∴P(-3,3,4).
∵n·![]() =0,n·
=0,n·![]() =0,
=0,
∴![]() 解得
解得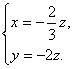
∴n=(-![]() ,-2,1)z.
,-2,1)z.
又AA1⊥平面ABCD,![]() =(0,0,6),
=(0,0,6),
∴n·![]() =6z,
=6z,
|n|=![]() z,
z,
|![]() |=6.
|=6.
∴cos〈n,![]() 〉=
〉= =±
=±![]() .
.
∵所求的二面角为锐角,
故平面AB1P与平面ABCD所成二面角的余弦值为![]() .
.
(3)∵cos〈![]() ,
,![]() 〉=
〉=![]() ,
,
∴cos〈![]() ,
,![]() 〉=
〉=![]() .依题意,得cos〈
.依题意,得cos〈![]() ,
,![]() 〉=cos〈
〉=cos〈![]() ,
,![]() 〉,
〉,
即3+2a=3![]() ,亦即a=
,亦即a=![]() ×6=
×6=![]() CC1.
CC1.
故P距C点的距离是侧棱的![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点. 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.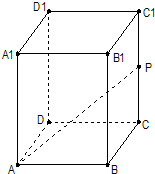 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)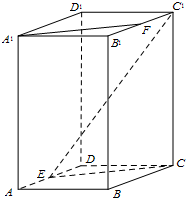 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.