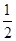题目内容
实数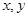 满足不等式组
满足不等式组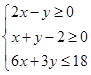 ,且
,且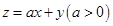 取最小值的最优
取最小值的最优
解有无穷多个, 则实数a的取值是 ( )
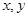 满足不等式组
满足不等式组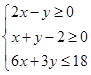 ,且
,且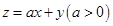 取最小值的最优
取最小值的最优解有无穷多个, 则实数a的取值是 ( )
A.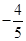 | B.1 | C.2 | D.无法确定 |
B
解:∵z=ax+y则y=-ax+z,z为直线y=-ax+z在y轴上的截距
要使目标函数取得最小值的最优解有无穷多个,则截距最小时的最优解有无数个
∵a>0把ax+y=z平移,使之与可行域中最左侧的点的边界AC重合即可,
∴-a=-1∵a=1故选B
要使目标函数取得最小值的最优解有无穷多个,则截距最小时的最优解有无数个
∵a>0把ax+y=z平移,使之与可行域中最左侧的点的边界AC重合即可,
∴-a=-1∵a=1故选B

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
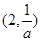 在直线
在直线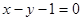 的左上方,则实数
的左上方,则实数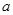 的取值范围是
的取值范围是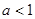
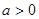

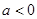 或
或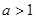
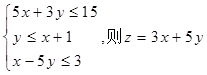 的最大值为
的最大值为 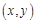 满足
满足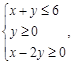 则
则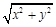 的最大值为( )
的最大值为( )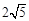
 满足线性约束条件
满足线性约束条件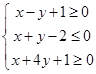 ,若
,若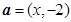 ,
,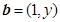 ,则
,则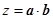 的最大值是( )
的最大值是( )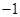
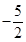
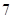
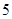
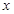 ,
,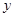 满足不等式组
满足不等式组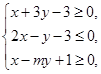 且
且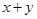 的最大值为9,则实数
的最大值为9,则实数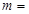 ( )
( )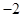
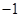
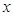 ,
,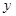 满足约束条件
满足约束条件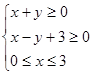 ,则
,则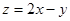 的最大值为( )
的最大值为( )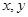 满足约束条件
满足约束条件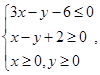 若目标函数
若目标函数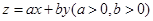 的最大值为12,则
的最大值为12,则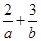 的最小值为
的最小值为
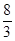
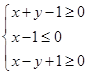 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )