题目内容
某中学从高中三个年级选派4名教师和20名学生去当文明交通宣传志愿者,20名学生的名额分配为高一12人,高二6人,高三2人.
(1)若从20名学生中选出3人做为组长,求他们中恰好有1人是高一年级学生的概率;
(2)若将4名教师随机安排到三个年级(假设每名教师加入各年级是等可能的,且各位教师的选择是相互独立的),记安排到高一年级的教师人数为X,求随机变量X的分布列和数学期望.
(1) 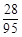 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)从高一12人中选出1人,从高二和高三共8人中选出2人的事件为A,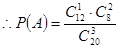 ,计算得到结果;(2)每位教师选择高一年级的概率均为
,计算得到结果;(2)每位教师选择高一年级的概率均为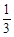 ,并且相互独立,X的所有取值为0,1,2,3,4.
,并且相互独立,X的所有取值为0,1,2,3,4.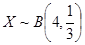 ,
, ,
,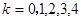 ,然后列出随机变量X的概率分布列,利用
,然后列出随机变量X的概率分布列,利用 ,或是利用二项分布的期望公式
,或是利用二项分布的期望公式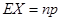 ,得出结果.随机变量的概率,分布列,期望还是高考的重点内容,属于基础题型,
,得出结果.随机变量的概率,分布列,期望还是高考的重点内容,属于基础题型,
试题解析:(1)解:设 “他们中恰好有1人是高一年级学生” 为事件 ,
,
则  .
.
所以恰好有1人是高一年级学生的概率为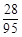 . 4分
. 4分
(2)解:X的所有取值为0,1,2,3,4. 6分
由题意可知,每位教师选择高一年级的概率均为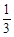 , 7分
, 7分
所以 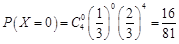 ;
;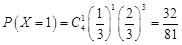
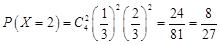 ;
;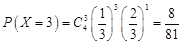 ;
;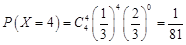 .
.
随机变量X的分布列为:
12分X 0 1 2 3 4 P 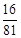
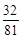
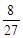
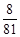
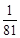
所以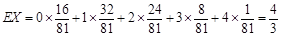 . 13分
. 13分
考点:1.超几何分布;2.二项分布.

 阅读快车系列答案
阅读快车系列答案甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 4 | 12 | 42 | 32 | 10 |
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=
 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)  ,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
 ,道路C,E上下班时间往返出现拥堵的概率都是
,道路C,E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
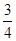 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击. 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取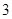 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中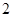 题便通过考查.已知
题便通过考查.已知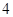 题能正确完成,
题能正确完成,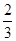 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.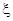 和文科考生乙正确完成题数
和文科考生乙正确完成题数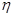 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望;