题目内容
已知椭圆
(a＞b＞0)的两个焦点为F1，F2，过F2作垂直于x轴的直线与椭圆相交，一个交点为P，若∠PF1F2=30°，那么椭圆的离心率是（ ）A.sin30°B.cos30°C.tan30°D.sin45°
解析：不妨设F 2为右焦点，则|PF 2|=,?
∴tan30°=
=
,即
?
e2+2e-
=0，?
∴e=
=tan30°,e=-
(舍)
答案：C
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
(a＞b＞0)的离心率为
,
，则椭圆方程为（ ）
Ｂ.
Ｄ.
(a>b>0)，A、B是椭圆上的两点，线段AB的垂直平分线与x轴相交于点P(x0，0)．证明
．已知椭圆
(a>b>0)抛物线
，从每条曲线上取两个点，将其坐标记录于下表中：
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
（1）求
的标准方程；（2）四边形ABCD的顶点在椭圆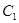
上，且对角线AC、BD过原点O，若
,
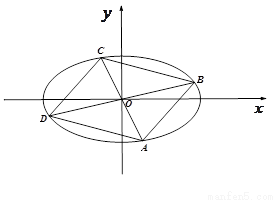
(i) 求
的最值.
(ii) 求四边形ABCD的面积；
(a>b>0)的左、右焦点分别为Fl vF2
,离心率
,A为右顶点,K为右准线与x轴的交点，且
.
的垂心?若存在,求出l的方程;若不存在,请说明理由.