题目内容
已知椭圆![]() (a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明
(a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明![]() .
.
证明见解析
解析:
本小题考查椭圆性质、直线方程等知识,以及综合分析能力.
证法一:设A、B的坐标分别为(x1,y1)和(x2,y2).因线段AB的垂直平分线与x轴相交,故AB不平行于y轴,即x1≠x2.又交点为P(x0,0),故|PA|=|PB|,即
(x1-x0)2+![]() =(x2-x0)2+
=(x2-x0)2+![]() ①
①
∵ A、B在椭圆上,∴![]() ,
, ![]() .
.
将上式代入①,得2(x2-x1) x0=![]() ②
②
∵ x1≠x2,可得![]() ③
③
∵ -a≤x1≤a,-a≤x2≤a,且x1≠x2,∴ -2a<x1+x2<2a,
∴ ![]()
证法二:设A、B的坐标分别为(x1,y1)和(x2,y2).因P(x0,0)在AB的垂直平分线上,以点P为圆心,|PA|=r为半径的圆P过A、B两点,圆P的方程为(x-x0)2+y2=r2,
与椭圆方程联立,消去y得(x-x0)2![]() x2=r2-b2,
x2=r2-b2,
∴![]() ①
①
因A、B是椭圆与圆P的交点,故x1,x2为方程①的两个根.由韦达定理得
x1+x2=![]() x0.
x0.
因-a≤x1≤a,-a≤x2≤a,且x1≠x2,故-2a<x1+x2=![]() x0<2a,
x0<2a,
∴ ![]()

已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆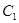 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
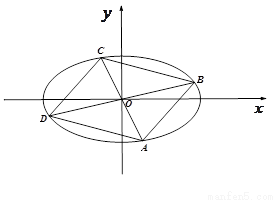
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
已知椭圆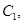
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:

|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;
的标准方程;
(2)四边形ABCD的顶点在椭圆 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线









 (a>b>0)的左、右焦点分别为Fl vF2
,离心率
(a>b>0)的左、右焦点分别为Fl vF2
,离心率 ,A为右顶点,K为右准线与x轴的交点,且
,A为右顶点,K为右准线与x轴的交点,且 .
. 的垂心?若存在,求出l的方程;若不存在,请说明理由.
的垂心?若存在,求出l的方程;若不存在,请说明理由.