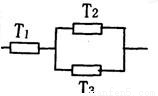
题目内容
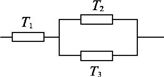 三个元件T1,T2,T3正常工作的概率分别为
三个元件T1,T2,T3正常工作的概率分别为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
分析:根据题意,记T1正常工作为事件A,T2正常工作为事件B,记T3正常工作为事件C,易得则P(A)、P(B)、P(C),若电路不发生故障,必须是T1正常工作且T2,T2至少有一个正常工作,由对立事件的概率性质可得T2,T2至少有一个正常工作的概率为1-P(
),计算可得其概率,由相互独立事件的概率乘法公式计算可得答案.
. |
| B |
. |
| C |
解答:解:记T1正常工作为事件A,T2正常工作为事件B,记T3正常工作为事件C,
则P(A)=
,P(B)=P(C)=
;
电路不发生故障,即T1正常工作且T2,T3至少有一个正常工作,
T2、T3不发生故障即T2,T3至少有一个正常工作的概率P1=1-P(
)=1-(1-
)(1-
)=
,
所以整个电路不发生故障的概率为P=P(A)×P1=
×
=
,
故选A.
则P(A)=
| 1 |
| 2 |
| 3 |
| 4 |
电路不发生故障,即T1正常工作且T2,T3至少有一个正常工作,
T2、T3不发生故障即T2,T3至少有一个正常工作的概率P1=1-P(
. |
| B |
. |
| C |
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 16 |
所以整个电路不发生故障的概率为P=P(A)×P1=
| 1 |
| 2 |
| 15 |
| 16 |
| 15 |
| 32 |
故选A.
点评:本题主要考查概率知识及实际应用能力,注意结合物理电学知识,分析电路解题.

练习册系列答案
相关题目
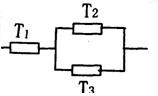 三个元件T1、T2、T3正常工作的概率分别为
三个元件T1、T2、T3正常工作的概率分别为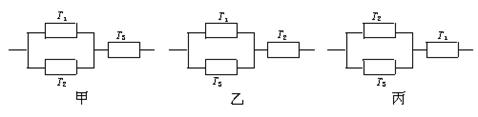
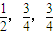 ,将它们中某两个元件并联后再和第三个元件串连接入电路,在如图的电路中,电路不发生故障的概率是( )
,将它们中某两个元件并联后再和第三个元件串连接入电路,在如图的电路中,电路不发生故障的概率是( )
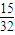
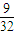
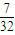
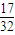
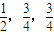 ,将它们中某两个元件并联后再和第三元件串连接入电路.
,将它们中某两个元件并联后再和第三元件串连接入电路.