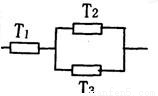
题目内容
三个元件T1、T2、T3正常工作的概率分别为0.7、0.8、0.9，将它们的某两个并联再和第三个串联接入电路，如图甲、乙、丙所示，问哪一种接法使电路不发生故障的概率最大？
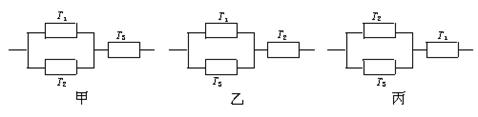
图甲的接法电路不发生故障的概率最大.
解析:
设元件T1、T2、T3能正常工作的事件为A1、A2、A3，电路不发生故障的事件为A，则P（A1）=0.7，P（A2）=0.8，P（A3）=0.9.
（1）按图甲的接法求P（A）: A=（A1+A2）·A3，
由A1+A2与A3相互独立，则P（A）=P（A1+A2）·P（A3）
又P（A1+A2）=1–P（
）=1–P（
·
）
由A1与A2相互独立知与相互独立，得:
P（·）=P（）·P（）=［1–P（A1）］·［1–P（A2）］
=（1–0.7）×(1–0.8)=0.06，∴P(A1+A2)=0.1–P(·)=1–0.06=0.94，
∴P(A)=0.94×0.9=0.846.
(2)按图乙的接法求P（A）
A=（A1+A3）·A2且A1+A3与A2相互独立，则P（A）=P（A1+A3）·P（A2），
用另一种算法求P（A1+A3）.
∵A1与A3彼此不互斥，
根据容斥原理P（A1+A3）=P（A1）+P（A3）–P（A1A3），
∵A1与A3相互独立，
则P（A1·A3）=P（A1）·P（A3）=0.7×0.9=0.63,P(A1+A3)
=0.7+0.9–0.63=0.97
∴P(A)=P(A1+A3)·P(A2)=0.97×0.8=0.776.
(3)按图丙的接法求P（A），用第三种算法.
A=（A2+A3）A1=A2A1+A3A1,
∵A2A1与A3A1彼此不互斥，
据容斥原理，则P（A）=P（A1A2）+P（A1A3）–P（A1A2A3），
又由A1、A2、A3相互独立，得P（A1·A2）=P（A1）P（A2）=0.8×0.7=0.56,
P(A3A1)=P(A3)·P(A1)=0.9×0.7=0.63,
P(A1A2A3)=P(A1)·P(A2)·P(A3)=0.7×0.8×0.9=0.504,
∴P(A)=0.56+0.63–0.504=0.686.
综合（1）、（2）、（3）得，图甲、乙、丙三种接法电路不发生故障的概率值分别为0.846,0.776,0.686.故图甲的接法电路不发生故障的概率最大.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案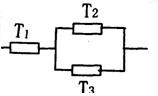
三个元件T1、T2、T3正常工作的概率分别为
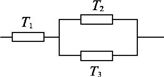三个元件T1，T2，T3正常工作的概率分别为
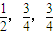，将它们中某两个元件并联后再和第三个元件串连接入电路，在如图的电路中，电路不发生故障的概率是（ ）
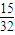
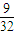
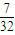
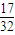
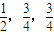，将它们中某两个元件并联后再和第三元件串连接入电路．