题目内容
函数f(x)=x+a与y=logax图象只可能是下图中的
- A.
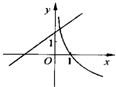
- B.
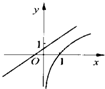
- C.
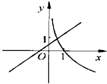
- D.
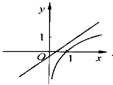
C
分析:当a>1时,根据一次函数、对数函数的图象和性质可得没有满足条件的选项.当1>a>0时,根据直线过定点以及对数函数的单调性判断只有C满足条件,从而得出结论.
解答:当a>1时,函数f(x)=x+a的图象时一条直线,斜率等于1,与y轴的交点(0,a),在点(0,1)的上方,
y=logax 是定义域内的增函数,图象从左到右是上升的,没有满足条件的选项.
当1>a>0时,函数f(x)=x+a的图象时一条直线,斜率等于1,与y轴的交点(0,a),在点(0,1)的下方,
y=logax 是定义域内的减函数,图象从左到右是下降的,只有C满足条件的选项.
故选C.
点评:本题主要考查一次函数、对数函数的图象和性质,以及数形结合能力,体现了分类讨论的数学思想,属于基础题.
分析:当a>1时,根据一次函数、对数函数的图象和性质可得没有满足条件的选项.当1>a>0时,根据直线过定点以及对数函数的单调性判断只有C满足条件,从而得出结论.
解答:当a>1时,函数f(x)=x+a的图象时一条直线,斜率等于1,与y轴的交点(0,a),在点(0,1)的上方,
y=logax 是定义域内的增函数,图象从左到右是上升的,没有满足条件的选项.
当1>a>0时,函数f(x)=x+a的图象时一条直线,斜率等于1,与y轴的交点(0,a),在点(0,1)的下方,
y=logax 是定义域内的减函数,图象从左到右是下降的,只有C满足条件的选项.
故选C.
点评:本题主要考查一次函数、对数函数的图象和性质,以及数形结合能力,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目