题目内容
已知函数f(x)=1-2ax-a2x(0<a<1)
(1)求函数f(x)的值域;
(2)若x∈[-2,1]时,函数f(x)的最小值为-7,求a的值和函数f(x) 的最大值.
解:(1)令t=ax,则t>0,∴g(t)=1-2t-t2=-(t+1)2+2
∵t>0,∴g(t)<1,即函数f(x)的值域为(-∞,1);
(2)∵x∈[-2,1],0<a<1,∴t∈[a, ]
]
∴g(t)=1-2t-t2在[a, ]上是减函数
]上是减函数
∴t= 时,g(t)min=-
时,g(t)min=- -
- +1=-7
+1=-7
∴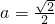 或
或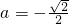 (舍去)
(舍去)
∴t=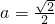 时,g(t)有最大值,即g(t)max=
时,g(t)有最大值,即g(t)max= -
- .
.
分析:(1)利用换元法,再进行配方,即可求得函数f(x)的值域;
(2)原因,求得函数的单调性,利用函数f(x)的最小值为-7,可求a的值,从而可得函数f(x) 的最大值.
点评:本题考查函数的最值与值域,考查学生的计算能力,属于中档题.
∵t>0,∴g(t)<1,即函数f(x)的值域为(-∞,1);
(2)∵x∈[-2,1],0<a<1,∴t∈[a,
 ]
]∴g(t)=1-2t-t2在[a,
 ]上是减函数
]上是减函数∴t=
 时,g(t)min=-
时,g(t)min=- -
- +1=-7
+1=-7∴
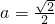 或
或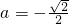 (舍去)
(舍去)∴t=
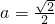 时,g(t)有最大值,即g(t)max=
时,g(t)有最大值,即g(t)max= -
- .
.分析:(1)利用换元法,再进行配方,即可求得函数f(x)的值域;
(2)原因,求得函数的单调性,利用函数f(x)的最小值为-7,可求a的值,从而可得函数f(x) 的最大值.
点评:本题考查函数的最值与值域,考查学生的计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|