题目内容
若函数 f(x)=(k-2)x2+(k-1)x+3是偶函数,则f(x)的递减区间是 .
(0,+ );
);
解析试题分析:因为函数 f(x)=(k-2)x2+(k-1)x+3是偶函数,所以,k=1,此时f(x)="-" x2
+3,图象开口向下,对称轴为y轴,故其单调减区间为(0,+ )。
)。
考点:本题主要考查函数的奇偶性、单调性。
点评:简单题,二次函数为偶函数,则x系数为0,通过确定函数图象的开口方向及对称轴,明确单调区间。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 上的奇函数
上的奇函数 ,当
,当 时,
时, ,那么
,那么 时,
时, .
. 在
在 上是单调递增函数,则
上是单调递增函数,则 的取值范围是_____________。
的取值范围是_____________。 的函数是 .
的函数是 .


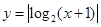
 ,则
,则 的解析式为 .
的解析式为 . 上单调递增的函数是 .
上单调递增的函数是 . ②
② ③
③ ④
④
 的定义域为
的定义域为  ,
,  ,
, 的大小关系是
的大小关系是