题目内容
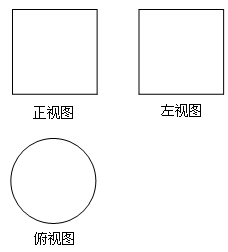
一个几何体的三视图如图所示,则该几何体的体积为
| A.2 | B.1 | C.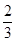 | D.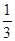 |
C
解析试题分析:由三视图可知该几何体是一个四棱锥,其底面是一个对角线为2的正方形,高为1,故其底面面积S=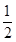 ×2×=2,则V=
×2×=2,则V=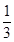 •Sh=
•Sh=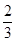 ,故选C.
,故选C.
考点:由三视图求面积、体积.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D—ABC的体积为( )
A. | B. | C. | D. |
下列几何体各自的三视图,其中有且仅有两个三视图完全相同的是( )
| A.①② | B.②④ | C.①③ | D.①④ |
一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几体的体积为( )
| A.6 |
| B.9 |
| C.12 |
| D.18 |
一个几何体的三视图如图所示,则该几何体的体积是
| A.112 | B.80 | C.72 | D.64 |
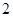 的正方形,俯视图是一个直径为
的正方形,俯视图是一个直径为