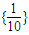题目内容
已知集合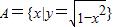 ,B={y|y=x2+1},则A∩B= .
,B={y|y=x2+1},则A∩B= .
【答案】分析:根据函数的定义域及其求法,我们可以求出集合A,根据二次函数的值域,我们可以求出集合B,代入集合的交集运算,即可得到答案.
解答:解:要使函数 的解析式有意义
的解析式有意义
x∈[-1,1]
故A=[-1,1]
又∵y=x2+1≥1
∴B={y|y=x2+1}=[1,+∞)
故A∩B={1}
故答案为:{1}
点评:本题考查的知识点是集合的交集及其运算,函数的定义域及其求法,二次函数的性质,其中根据函数定义域和值域的求法,分别求出集合A,B是解答本题的关键.
解答:解:要使函数
 的解析式有意义
的解析式有意义x∈[-1,1]
故A=[-1,1]
又∵y=x2+1≥1
∴B={y|y=x2+1}=[1,+∞)
故A∩B={1}
故答案为:{1}
点评:本题考查的知识点是集合的交集及其运算,函数的定义域及其求法,二次函数的性质,其中根据函数定义域和值域的求法,分别求出集合A,B是解答本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
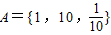 ,B={y|y=lgx,x∈A},则A∩B=( )
,B={y|y=lgx,x∈A},则A∩B=( )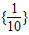
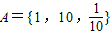 ,B={y|y=lgx,x∈A},则A∩B=( )
,B={y|y=lgx,x∈A},则A∩B=( )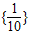
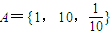 ,B={y|y=lgx,x∈A},则A∩B=( )
,B={y|y=lgx,x∈A},则A∩B=( )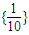
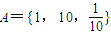 ,B={y|y=lgx,x∈A},则A∩B=( )
,B={y|y=lgx,x∈A},则A∩B=( )