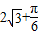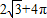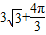题目内容
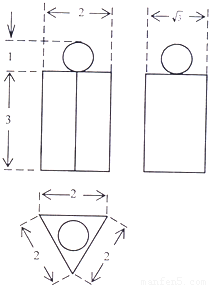
 如图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,求该几何体的表面积及体积.
如图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,求该几何体的表面积及体积.分析:由该几何体的三视图知该几何体是底面是边长为2的等边三角形,高为4的三棱柱,由此能求出该几何体的表面积及体积.
解答:解:由该几何体的三视图知:
该几何体是底面是边长为2的等边三角形,高为4的三棱柱,
∴该几何体的表面积S=3×(4×2)+2×(
×2×2×sin60°)=24+2
.(4分)
该几何体的体积V=(
×2×2×sin60°)×4=4
.(4分)
该几何体是底面是边长为2的等边三角形,高为4的三棱柱,
∴该几何体的表面积S=3×(4×2)+2×(
| 1 |
| 2 |
| 3 |
该几何体的体积V=(
| 1 |
| 2 |
| 3 |
点评:本题考查利用几何体的三视图,求几何体的表面积和体积,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )
(2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )