题目内容
 设A、B为函数
设A、B为函数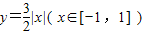 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点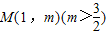 ,已知M是线段BC的中点.
,已知M是线段BC的中点.(1)设点B的横坐标为t,写出△ABC的面积S关于t的函数S=f(t)的表达式;
(2)求函数S=f(t)的最大值,并求此时点C的坐标.
【答案】分析:(1)假设B的坐标,利用M是线段BC的中点,可得点C的坐标,从而可得△ABC的面积S关于t的函数S=f(t)的表达式;
(2)先配方,再分类讨论,即可求得函数S=f(t)的最大值,及此时点C的坐标.
解答:解:(1)如图,设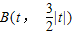 ,由M是线段BC的中点,且
,由M是线段BC的中点,且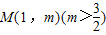 ,可得点C的坐标为
,可得点C的坐标为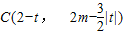 .
.
∴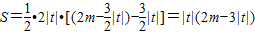
即: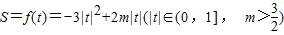 …(6分)
…(6分)
(2)由上知: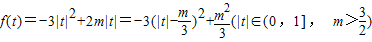
①当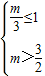 即
即 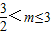 时,令
时,令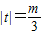 ,f(t)有最大值
,f(t)有最大值 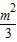 ,
,
此时,点C的坐标为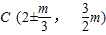 ;
;
②当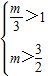 即 m>3时,令|t|=1,f(t)有最大值 2m-3,此时,点C的坐标为
即 m>3时,令|t|=1,f(t)有最大值 2m-3,此时,点C的坐标为  或
或 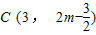 ….(12分)
….(12分)
综上,当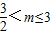 时,f(t)有最大值
时,f(t)有最大值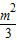 ,此时,点C的坐标为
,此时,点C的坐标为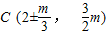 ;当m>3时,f(t)有最大值2m-3,此时,点C的坐标为
;当m>3时,f(t)有最大值2m-3,此时,点C的坐标为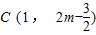 或
或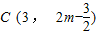 …(13分)
…(13分)
点评:本题考查三角形面积的计算,考查函数的最值,考查配方法的运用,考查分类讨论的数学思想,属于中档题.
(2)先配方,再分类讨论,即可求得函数S=f(t)的最大值,及此时点C的坐标.
解答:解:(1)如图,设
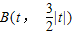 ,由M是线段BC的中点,且
,由M是线段BC的中点,且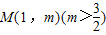 ,可得点C的坐标为
,可得点C的坐标为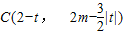 .
.∴
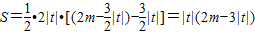
即:
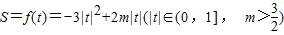 …(6分)
…(6分)(2)由上知:
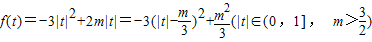
①当
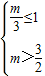 即
即 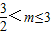 时,令
时,令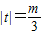 ,f(t)有最大值
,f(t)有最大值 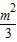 ,
,此时,点C的坐标为
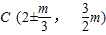 ;
;②当
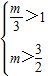 即 m>3时,令|t|=1,f(t)有最大值 2m-3,此时,点C的坐标为
即 m>3时,令|t|=1,f(t)有最大值 2m-3,此时,点C的坐标为  或
或 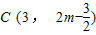 ….(12分)
….(12分)综上,当
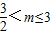 时,f(t)有最大值
时,f(t)有最大值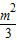 ,此时,点C的坐标为
,此时,点C的坐标为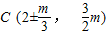 ;当m>3时,f(t)有最大值2m-3,此时,点C的坐标为
;当m>3时,f(t)有最大值2m-3,此时,点C的坐标为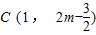 或
或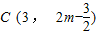 …(13分)
…(13分)点评:本题考查三角形面积的计算,考查函数的最值,考查配方法的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
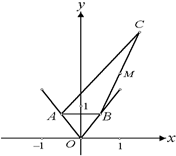 设A、B为函数
设A、B为函数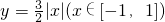 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点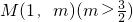 ,已知M是线段BC的中点.
,已知M是线段BC的中点.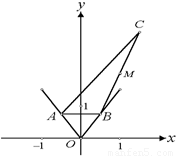 设A、B为函数
设A、B为函数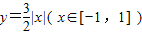 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点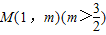 ,已知M是线段BC的中点.
,已知M是线段BC的中点. 设A、B为函数
设A、B为函数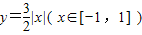 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点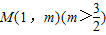 ,已知M是线段BC的中点.
,已知M是线段BC的中点.