题目内容
已知向量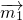 =(0,x),
=(0,x), =(1,1),
=(1,1),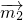 =(x,0),
=(x,0), =(y2,1)(其中x,y是实数),又设向量
=(y2,1)(其中x,y是实数),又设向量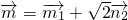 ,
,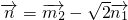 ,且
,且 ,点P(x,y)的轨迹为曲线C.
,点P(x,y)的轨迹为曲线C.
(1)求曲线C的方程;
(2)设曲线C与y轴的正半轴的交点为M,过点M作一条直线l与曲线C交于另一点N,当|MN|= 时,求直线 l 的方程.
时,求直线 l 的方程.
解:(1)由已知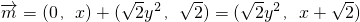
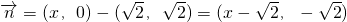 ,(2分)
,(2分)
∵ ,∴
,∴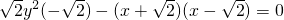 (4分)
(4分)
即所求曲线C的方程是: (6分)
(6分)
(2)由(1)求得点M(0,1).显然直线l与x轴不垂直.
故可设直线l的方程为y=kx+1,设M(x1,y1),N(x2,y2)(8分)
由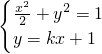 ,消去y得:(1+2k2)x2+4kx=0,解得
,消去y得:(1+2k2)x2+4kx=0,解得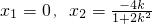 .(10分)
.(10分)
由|MN|=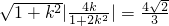 ,解得:k=±1(12分)
,解得:k=±1(12分)
∴所求直线的方程为x-y+1-0或x+y-1=0.(14分)
分析:(1)由已知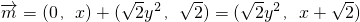 ,
,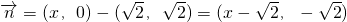 ,由
,由 ,能导出所求曲线C的方程.
,能导出所求曲线C的方程.
(2)由点M(0,1),知直线l与x轴不垂直.设直线l的方程为y=kx+1,设M(x1,y1),N(x2,y2),由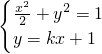 ,得(1+2k2)x2+4kx=0,由此能得到所求直线的方程.
,得(1+2k2)x2+4kx=0,由此能得到所求直线的方程.
点评:本题考查直线方程和曲线方程的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
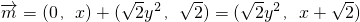
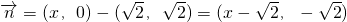 ,(2分)
,(2分)∵
 ,∴
,∴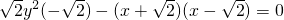 (4分)
(4分)即所求曲线C的方程是:
 (6分)
(6分)(2)由(1)求得点M(0,1).显然直线l与x轴不垂直.
故可设直线l的方程为y=kx+1,设M(x1,y1),N(x2,y2)(8分)
由
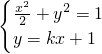 ,消去y得:(1+2k2)x2+4kx=0,解得
,消去y得:(1+2k2)x2+4kx=0,解得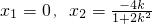 .(10分)
.(10分)由|MN|=
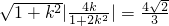 ,解得:k=±1(12分)
,解得:k=±1(12分)∴所求直线的方程为x-y+1-0或x+y-1=0.(14分)
分析:(1)由已知
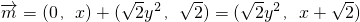 ,
,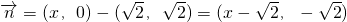 ,由
,由 ,能导出所求曲线C的方程.
,能导出所求曲线C的方程.(2)由点M(0,1),知直线l与x轴不垂直.设直线l的方程为y=kx+1,设M(x1,y1),N(x2,y2),由
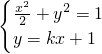 ,得(1+2k2)x2+4kx=0,由此能得到所求直线的方程.
,得(1+2k2)x2+4kx=0,由此能得到所求直线的方程.点评:本题考查直线方程和曲线方程的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
(中数量积)已知向量
,
,x,y满足|
|=|
|=1,
•
=0,且
,则|
|+|
|等于( )
| a |
| b |
| a |
| b |
| a |
| b |
|
| x |
| y |
A、
| ||||
B、
| ||||
| C、2 | ||||
| D、5 |