题目内容
在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=
，E为AB上一个动点，则D1E+CE的最小值为（ ）
| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、x≤y |
分析：画出几何体的图形，连接D1A延长至G使得AG=AD，连接C1B延长至F使得BF=BC，连接EF，D1F，则D1F为所求．
解答：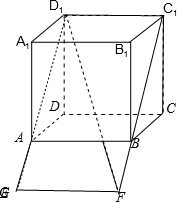
解：画出几何体的图形，连接D1A延长至G使得AG=AD，
连接C1B延长至F使得BF=BC，连接EF，则ABFG为正方形，
连接D1F，则D1F为D1E+CE的最小值：D1F=
=
=
故选B．
解：画出几何体的图形，连接D1A延长至G使得AG=AD，连接C1B延长至F使得BF=BC，连接EF，则ABFG为正方形，
连接D1F，则D1F为D1E+CE的最小值：D1F=
| GF2+D1G2 |
| 12+( 3)2 |
| 10 |
故选B．
点评：本题是中档题，考查正四棱柱表面距离的最小值问题，考查折叠与展开的关系，能够转化为平面上两点的距离是解题的关键，考查空间想象能力，计算能力．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
如图，在正四棱柱ABCD-A1B1C1D1中，棱长AA1=2，AB=1，E是AA1的中点．
在正四棱柱ABCD-A1B1C1D1中，AA1=2AB，E为CC1的中点．
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=2，M、N分别为B1B和A1D的中点．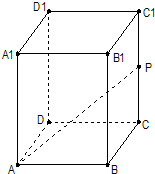
（2012•长宁区一模）在正四棱柱ABCD-A1B1C1D1中，已知底面ABCD的边长为2，点P是CC1的中点，直线AP与平面BCC1B1成30°角，求异面直线BC1和AP所成角的大小．（结果用反三角函数值表示）
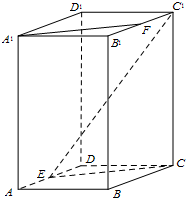（2012•昌平区二模）在正四棱柱ABCD-A1B1C1D1中，E为AD中点，F为B1C1中点．