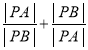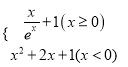题目内容
【题目】已知函数
（
）在
上至少存在两个不同的
，
满足
，且
在
上具有单调性，点
和直线
分别为图象的一个对称中心和一条对称轴，则下列命题中正确的是（ ）
A.的最小正周期为
B.
C.在
上是减函数
D.将图象上每一点的横坐标伸长为原来的2倍（纵坐标不变），得到
的图象，则
【答案】BC
【解析】
由对称中心和对称轴方程，可得
，由题意可得
，结合三角函数的周期性和单调性，图像平移变换可得所求结论.
由题意可得
，即
可得
在
上至少存在两个最大值或最小值，且在
具有单调性
当
时，解方程可得
的最小正周期为
，故A不正确；
，故B正确；
由于
可得减区间为
可得在
上是减函数，故C正确；
将图像上每一点的横坐标伸长为原来的2倍（纵坐标不变），得到
的图像，可得
，故D错误.
故选：BC
【题目】为了打好脱贫攻坚战，某贫困县农科院针对玉米种植情况进行调研，力争有效地改良玉米品种，为农民提供技术支援，现对已选出的一组玉米的茎高进行统计，获得茎叶图如图（单位：厘米），设茎高大于或等于180厘米的玉米为高茎玉米，否则为矮茎玉米．
（1）求出易倒伏玉米茎高的中位数
；
（2）根据茎叶图的数据，完成下面的列联表：
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
（3）根据（2）中的列联表，是否可以在犯错误的概率不超过1%的前提下，认为抗倒伏与玉米矮茎有关？
附：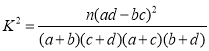
，
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】4月23日是“世界读书日”，某中学开展了一系列的读书教育活动．学校为了解高三学生课外阅读情况，采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组（每名学生只能参加一个读书小组）学生抽取12名学生参加问卷调查．各组人数统计如下：
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
（1）从参加问卷调查的12名学生中随机抽取2人，求这2人来自同一个小组的概率；
（2）从已抽取的甲、丙两个小组的学生中随机抽取2人，用
表示抽得甲组学生的人数，求随机变量的分布列和数学期望．
