题目内容
用[a]表示不大于实数a的最大整数,如[1.68]=1,设x1,x2分别是方程x+ex-4=0及x+ln(x-1)-4=0的根,则[x1]+[x2]=( )
分析:由题意可得,直线y=4-x和函数y=ex交点的横坐标为x1,直线y=4-x和函数y=ln(x-1)的交点的横坐标为x2,结合图象可得1<x1<2,3<x2<4,从而求出[x1],[x2]的值即可求出所求.
解答:解:∵x1,x2分别是方程x+2x=3及x+log2(x-1)=3的根,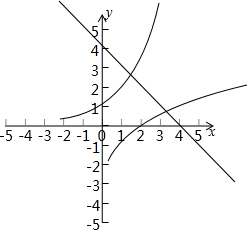
∴ex1=4-x1,且 ln(x2-1)=4-x2,故直线y=4-x和函数y=ex交点的横坐标为x1,
直线y=4-x和函数y=ln(x-1)的交点的横坐标为x2,
结合图象可得1<x1<2,3<x2<4,
∴[x1]=1,[x2]=3,
∴[x1]+[x2]=4,
故选C
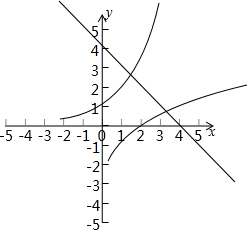
∴ex1=4-x1,且 ln(x2-1)=4-x2,故直线y=4-x和函数y=ex交点的横坐标为x1,
直线y=4-x和函数y=ln(x-1)的交点的横坐标为x2,
结合图象可得1<x1<2,3<x2<4,
∴[x1]=1,[x2]=3,
∴[x1]+[x2]=4,
故选C
点评:本题考查了根的存在性及根的个数判断,以及函数与方程的思想,解答关键是运用数形结合的思想,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
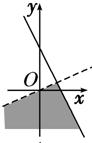
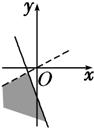
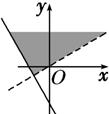
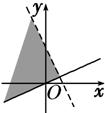
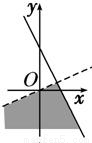
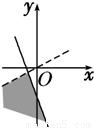
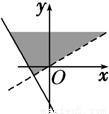
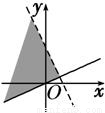
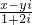 +i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为下图中的
+i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为下图中的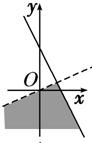
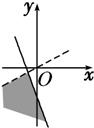
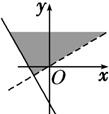
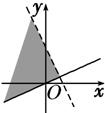
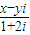 +i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为下图中的( )
+i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为下图中的( )