题目内容
渔场中鱼群的最大养殖量是m吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留出适当的空闲量。已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比,比例系数为k(k>0).
写出y关于x的函数关系式,指出这个函数的定义域;
求鱼群年增长量的最大值;
当鱼群的年增长量达到最大值时,求k的取值范围.
写出y关于x的函数关系式,指出这个函数的定义域;
求鱼群年增长量的最大值;
当鱼群的年增长量达到最大值时,求k的取值范围.
(1)y=kx(1-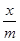 )定义域为{x|0<x<m
)定义域为{x|0<x<m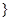 。
。
(2)鱼群年增长量的最大值为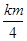 .
.
(3)0<k<2.
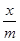 )定义域为{x|0<x<m
)定义域为{x|0<x<m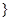 。
。(2)鱼群年增长量的最大值为
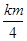 .
.(3)0<k<2.
试题分析:
思路分析:函数应用问题,要注意“审清题意,设出变量,列出关系式,解决数学问题,答”等解题步骤。
(1)注意理解空闲量为m-x吨,空闲率为
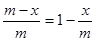 。
。 (2)利用二次函数的性质。
(3)特别注意利用“实际养殖量和年增长量之和小于最大养殖量”,建立不等式。
解:(1)因鱼群最大养殖量为m吨,实际养殖量为m吨,则空闲量为(m-x)吨,
空闲率为
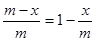 ,依题意,鱼群增长量为y=kx(1-
,依题意,鱼群增长量为y=kx(1-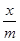 ),
),定义域为{x|0<x<m
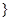 。
。(2)
 当x=m/2时,
当x=m/2时,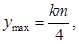

即鱼群年增长量的最大值为
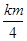 .
.(3)由于实际养殖量和年增长量之和小于最大养殖量,有0<x+y<m成立,
即0<
 ,得-2<k<2,但k>0,
,得-2<k<2,但k>0,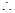 0<k<2.
0<k<2.点评:中档题,函数应用问题,要注意“审清题意,设出变量,列出关系式,解决数学问题,答”等解题步骤。由于是二次函数,处理最值问题时可依二次函数求最值得方法来求,而实际养殖量和年增长量之和小于最大养殖量应是常识,在阅读题意时要得到这个隐含条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
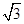 、圆心角为
、圆心角为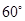 的扇形的弧上任取一点
的扇形的弧上任取一点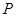 ,作扇形的内接矩形
,作扇形的内接矩形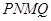 ,使点
,使点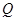 在
在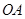 上,点
上,点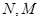 在
在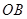 上,设矩形
上,设矩形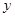 ,
,
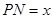 ,将
,将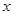 的函数关系式;
的函数关系式;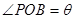 ,将
,将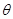 的函数关系式;
的函数关系式;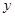 万元与投入
万元与投入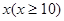 万元之间满足:
万元之间满足: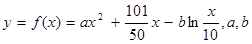 为常数。当
为常数。当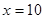 万元时,
万元时,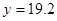 万元;
万元;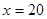 万元时,
万元时,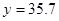 万元。 (参考数据:
万元。 (参考数据: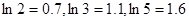 )
)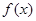 的解析式;
的解析式;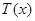 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。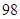 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出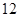 万元,第二年需要支出
万元,第二年需要支出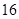 万元,第三年需要支出
万元,第三年需要支出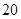 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出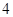 万元,而每年的生产收入都为
万元,而每年的生产收入都为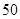 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用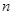 年,
年,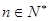 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这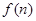 等于这
等于这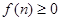 ,求
,求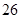 万元的价格出售该套设备;
万元的价格出售该套设备;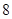 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.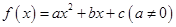 ,且不等式
,且不等式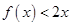 的解集为
的解集为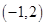 .
.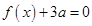 有两个相等的实根,求
有两个相等的实根,求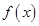 的解析式;
的解析式;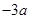 ,求实数
,求实数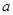 的取值范围;
的取值范围;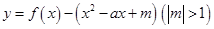 存在零点,并求出零点.
存在零点,并求出零点.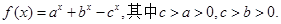
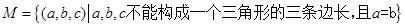 ,则
,则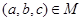 所对应的
所对应的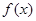 的零点的取值集合为 .
的零点的取值集合为 .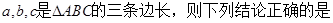 ______.(写出所有正确结论的序号)
______.(写出所有正确结论的序号)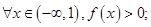
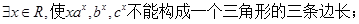
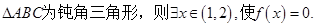
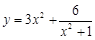 的最小值是
的最小值是 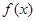 满足:
满足: (
(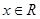 ),
),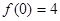 ,求
,求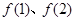 的值,并用数学归纳法证明:对任意的
的值,并用数学归纳法证明:对任意的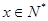 ,均有:
,均有: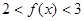 .
.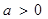 ,函数
,函数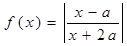 。
。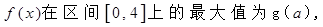 求
求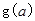 的表达式;
的表达式;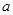 ,使函数
,使函数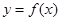 在区间
在区间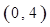 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求