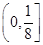题目内容
若圆 上至少有三个不同的点到直线
上至少有三个不同的点到直线 的距离为
的距离为 ,则直线
,则直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:先求出圆心和半径,比较半径和 ;要求圆上至少有三个不同的点到直线l:ax+by=0的距离为
;要求圆上至少有三个不同的点到直线l:ax+by=0的距离为 ,则圆心到直线的距离应小于等于
,则圆心到直线的距离应小于等于 ,用圆心到直线的距离公式,可求得结果.
,用圆心到直线的距离公式,可求得结果.
考点:直线和圆的位置关系.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
直线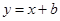 与曲线
与曲线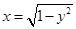 有且仅有1个公共点,则b的取值范围是( )
有且仅有1个公共点,则b的取值范围是( )
A.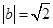 | B. 或 或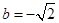 |
C.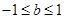 | D.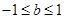 或 或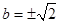 |
已知 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
| A.3 | B.5 | C.9 | D.25 |
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为( )
| A.(x+1)2+y2=2 | B.(x-1)2+y2=1 |
| C.(x+1)2+y2=4 | D.(x-2)2+y2=4 |
已知M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
已知圆(x+1)2+(y-1)2=1上一点P到直线3x-4y-3=0距离为d,则d的最小值为( ).
| A.1 | B.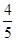 | C. | D.2 |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,半径为 的圆的方程为( ).
的圆的方程为( ).
| A.x2+y2-2x+4y=0 |
| B.x2+y2+2x+4y=0 |
| C.x2+y2+2x-4y=0 |
| D.x2+y2-2x-4y=0 |