题目内容
实数集A满足条件:若a∈A,则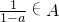 (a≠1).
(a≠1).
求证:①若2∈A,则A中必还有另外两个元素;
②集合A不可能是单元素集.
证明:①若a∈A,则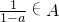 .
.
又∵2∈A,
∴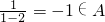
∵-1∈A,∴ .
.
∵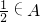 ,∴
,∴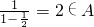 .
.
∴A中另外两个元素为-1,
②若A为单元素集,则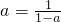 ,即a2-a+1=0,方程无解.
,即a2-a+1=0,方程无解.
∴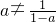 ,
,
∴A不可能为单元素集.
分析:①根据集合的互异性进行求解,注意条件2∈A,把2代入进行验证;
②可以假设A为单元素集合,求出其等价条件,从而进行判断;
点评:此题主要考查集合与元素之间的关系,注意集合内元素的互异性,是一道基础题.
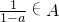 .
.又∵2∈A,
∴
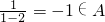
∵-1∈A,∴
 .
.∵
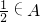 ,∴
,∴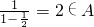 .
.∴A中另外两个元素为-1,

②若A为单元素集,则
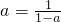 ,即a2-a+1=0,方程无解.
,即a2-a+1=0,方程无解.∴
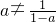 ,
,∴A不可能为单元素集.
分析:①根据集合的互异性进行求解,注意条件2∈A,把2代入进行验证;
②可以假设A为单元素集合,求出其等价条件,从而进行判断;
点评:此题主要考查集合与元素之间的关系,注意集合内元素的互异性,是一道基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
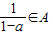 (a≠1).
(a≠1).