题目内容
设甲、乙、丙三人进行围棋比赛,每局两人参加,没有平局.在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 .比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束.
.比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束.(1)求只进行了三局比赛,比赛就结束的概率;
(2)记从比赛开始到比赛结束所需比赛的局数为ξ,求ξ的概率分布列和数学期望Eξ.
【答案】分析:(1)只进行三局比赛,即丙获胜比赛就结束,由互斥,独立事件的概率公式可得;(2)由题意可得ξ=2,3,4,分别可得其概率,可得分布列,可得期望.
解答:解:(1)由题意只进行三局比赛,即丙获胜比赛就结束,
故可得所求的概率为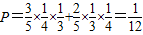
(2)由题意可得ξ=2,3,4,且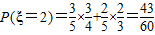 ,
,
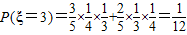 ,
,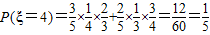
故ξ的分布列为:
故数学期望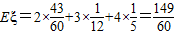
点评:本题考查离散型随机变量及其分布列,以及数学期望的求解,属中档题.
解答:解:(1)由题意只进行三局比赛,即丙获胜比赛就结束,
故可得所求的概率为
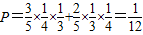
(2)由题意可得ξ=2,3,4,且
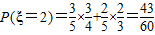 ,
,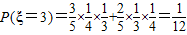 ,
,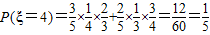
故ξ的分布列为:
| ξ | 2 | 3 | 4 |
| P | 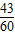 | 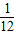 |  |
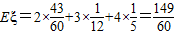
点评:本题考查离散型随机变量及其分布列,以及数学期望的求解,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
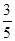 ,甲胜丙的概率为
,甲胜丙的概率为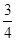 ,乙胜丙的概率为
,乙胜丙的概率为 。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。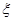 ,求
,求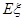 。
。