题目内容
已知抛物线的方程为y2=2px（p＞0），且抛物线上各点与焦点距离的最小值为2，若点M在此抛物线上运动，点N与点M关于点A（1，1）对称，则点N的轨迹方程为
- A.（x-2）2=-8（y-2）
- B.（x-2）2=8（y-2）
- C.（y-2）2=-8（x-2）
- D.（y-2）2=8（x-2）
C
分析：由抛物线上各点与焦点距离的最小值为2，先确定抛物线方程，再利用中点坐标公式寻找动点之间坐标关系，代入即可．
解答：由于抛物线上各点与焦点距离的最小值为2，∴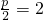
，∴2p=8，∴抛物线的方程为y2=8x
设点N（（x，y），则M（2-x，2-y），代入抛物线方程得：（y-2）2=-8（x-2），
故选C．
点评：本题考查了抛物线的几何形状，考查代入法求轨迹方程，应注意利用中点坐标公式寻找动点之间坐标关系．
分析：由抛物线上各点与焦点距离的最小值为2，先确定抛物线方程，再利用中点坐标公式寻找动点之间坐标关系，代入即可．
解答：由于抛物线上各点与焦点距离的最小值为2，∴
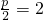，∴2p=8，∴抛物线的方程为y2=8x设点N（（x，y），则M（2-x，2-y），代入抛物线方程得：（y-2）2=-8（x-2），
故选C．
点评：本题考查了抛物线的几何形状，考查代入法求轨迹方程，应注意利用中点坐标公式寻找动点之间坐标关系．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
已知抛物线的方程为y=2ax2，且过点（1，4），则焦点坐标为（ ）
| A、（1，0） | ||
B、（
| ||
C、（0，
| ||
| D、（0，1） |
x2，则它的焦点坐标为（ ）