题目内容
19．函数y=-x2-2x+3（-5≤x≤2）的值域是[-12，4]．分析 配方得到y=-（x+1）2+4，根据-5≤x≤2便可求出f（x）的最大值和最小值，从而得出该函数的值域．
解答 解：y=-x2-2x+3=-（x+1）2+4；
∴x=-1时，y取最大值4；x=-5时，y取最小值-12；
∴该函数的值域为[-12，4]．
故答案为：[-12，4]．
点评 考查函数值域的概念，以及配方法求二次函数在闭区间上的值域．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
15．下列对应关系，不是数集M到数集N上的函数是（ ）
| A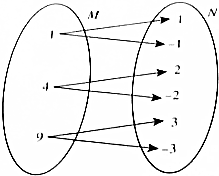． |  | B． |  | ||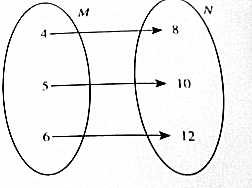
| C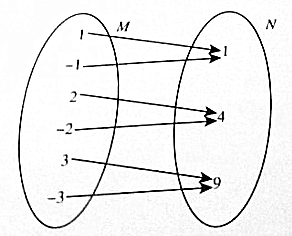． |  | D． |  |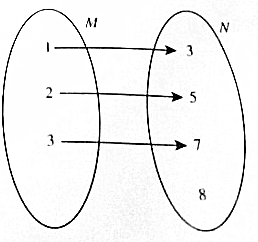
14．若f（x）是偶函数，当x＞0时，f（x）=x2-2x，则f（-$\frac{1}{2}$）=（ ）
| A． | $\frac{5}{4}$ | B． | $-\frac{5}{4}$ | C． | $\frac{3}{4}$ | D． | $-\frac{3}{4}$ |
8．数列2，3，4，5，…的一个通项公式为（ ）
| A． | an=n | B． | an=n+1 | C． | an=n+2 | D． | an=2n |
已知函数f（x）=|x2-2x|．