题目内容
把20个不加区别的小球放入编号为1,2,3的三个盒子中,要求每个盒子内的球数不小于它的编号数,则不同的放法共有____________种.
解析:不妨设编号为1,2,3的三个盒子中分别放入了x1,x2,x3个小球,依题意有
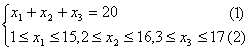
问题转化为在条件(2)下求不定方程(1)的解的个数,可考虑用分类计数的方法.
当x1=1时,x2=2,3, …,16,这时x3随之而定,从而共有15种放法.
当x1=2时,x2=2,3, …,15,这时x3随之而定,从而共有14种放法.
当x1=15时,只有x2=2,x3=3,仅有一种放法.
根据分类原理,符合要求的放法共有N=15+14+…+2+1=120(种).

练习册系列答案
相关题目