题目内容
某商场销售某种商品的经验表明，该商品每日的销售量y(单位：千克)与销售价格x(单位：元/千克)满足关系式y＝
＋10(x－6)2. 其中3<x<6，a为常数. 已知销售价格为5元/千克时，每日可售出该商品11千克.
（Ⅰ）求a的值；
（Ⅱ）若该商品的成本为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大.
（1）2；（2）当销售价格为4元/千克时，商场每日销售该商品所获得的利润最大.
【解析】本试题主要考查了函数在实际生活中的运用。第一问中，x＝5时，y＝11，所以，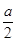
＋10＝11，a＝2，可得结论。第二问中，由(1)可知，该商品每日的销售量y＝
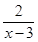＋10(x－6)2，所以商场每日销售该商品所获得的利润为
f(x)＝(x－3)[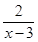＋10(x－6)2]＝2＋10(x－3)(x－6)2，（3<x<6）然后求导数，利用极值得到最值。
解：(Ⅰ)因为x＝5时，y＝11，所以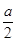，＋10＝11，a＝2. ………………………3分
(Ⅱ)由(1)可知，该商品每日的销售量y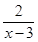＝＋10(x－6)2，
所以商场每日销售该商品所获得的利润为
f(x)＝(x－3)[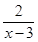＋10(x－6)2]＝2＋10(x－3)(x－6)2，（3<x<6） ……………………5分
从而，f′(x)＝10[(x－6)2＋2(x－3)(x－6)]＝30(x－4)(x－6)，
令f′(x)＝0，得x=4或x=6（舍去）. ………………………………………6分
因为当x∈(3，4)时，f′(x)>0，当x∈(4，6)时，f′(x)<0，
所以f (x)在(3，6)取得唯一的极大值，也就是最大值， …………………………………10分
所以，当x＝4时，函数f(x)取得最大值，且最大值等于42. ……………………11分
答：当销售价格为4元/千克时，商场每日销售该商品所获得的利润最大. …………12分
，其中3＜x＜6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．
，其中3＜x＜6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．
，其中3＜x＜6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．
，其中3＜x＜6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．