题目内容
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式 ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.(Ⅰ)求a的值
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
【答案】分析:(I)由f(5)=11代入函数的解析式,解关于a的方程,可得a值;
(II)商场每日销售该商品所获得的利润=每日的销售量×销售该商品的单利润,可得日销售量的利润函数为关于x的三次多项式函数,再用求导数的方法讨论函数的单调性,得出函数的极大值点,从而得出最大值对应的x值.
解答:解:(I)因为x=5时,y=11,所以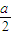 +10=11,故a=2
+10=11,故a=2
(II)由(I)可知,该商品每日的销售量y=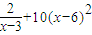
所以商场每日销售该商品所获得的利润为
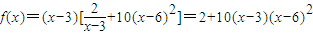
从而,f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-6)(x-4)
于是,当x变化时,f(x)、f′(x)的变化情况如下表:
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以,当x=4时,函数f(x)取得最大值,且最大值等于42
答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
点评:本题函数解析式的建立比较容易,考查的重点是利用导数解决生活中的优化问题,属于中档题.
(II)商场每日销售该商品所获得的利润=每日的销售量×销售该商品的单利润,可得日销售量的利润函数为关于x的三次多项式函数,再用求导数的方法讨论函数的单调性,得出函数的极大值点,从而得出最大值对应的x值.
解答:解:(I)因为x=5时,y=11,所以
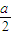 +10=11,故a=2
+10=11,故a=2(II)由(I)可知,该商品每日的销售量y=
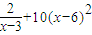
所以商场每日销售该商品所获得的利润为
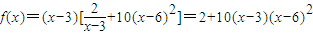
从而,f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-6)(x-4)
于是,当x变化时,f(x)、f′(x)的变化情况如下表:
| x | (3,4) | 4 | (4,6) |
| f'(x) | + | - | |
| f(x) | 单调递增 | 极大值42 | 单调递减 |
所以,当x=4时,函数f(x)取得最大值,且最大值等于42
答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
点评:本题函数解析式的建立比较容易,考查的重点是利用导数解决生活中的优化问题,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克. ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克. ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.