题目内容
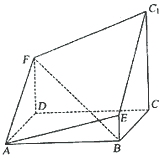
 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.(Ⅰ)求BF的长;
(Ⅱ)求二面角E-FC1-C的余弦值.
分析:(I)由长方体的几何特征,我们可以建立空间坐标系,设出F点的坐标,我们易根据截面AEC1F为平行四边形,
=
,得到F点的坐标;
(II)我们分别求出平面EFC1及平面FC1C的法向量,代入向量夹角公式,即可得到二面角E-FC1-C的余弦值.
| AF |
| EC1 |
(II)我们分别求出平面EFC1及平面FC1C的法向量,代入向量夹角公式,即可得到二面角E-FC1-C的余弦值.
解答: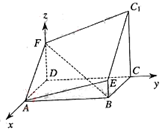 解:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0)A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3)设F(0,0,z).
解:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0)A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3)设F(0,0,z).
∵AEC1F为平行四边形,
∴
=
即(-2,0,z)=(-2,0,2),∴z=2.
∴F(0,0,2).
∴
=(-2,-4,2).于是|
|=2
,即BF的长为2
.
(II)设
为平面AEC1F的法向量且
=(x,y,z)
由
得
即
令z=1∴
平面FCC1的法向量为
=(-2,0,0)
设二面角E-FC1-C为α,则cosα=
=
=
.
 解:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0)A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3)设F(0,0,z).
解:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0)A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3)设F(0,0,z).∵AEC1F为平行四边形,
∴
| AF |
| EC1 |
即(-2,0,z)=(-2,0,2),∴z=2.
∴F(0,0,2).
∴
| EF |
| BF |
| 6 |
| 6 |
(II)设
| n1 |
| n1 |
由
|
|
|
|
| AD |
设二面角E-FC1-C为α,则cosα=
|
| ||||
|
|
| 2 | ||||
2×
|
4
| ||
| 33 |
点评:本题考查的知识点是二面角的平面角及求法,空间中点的坐标,其中(I)的关键是根据平行四边形法则,得到
=
,(II)的关键是求出平面EFC1及平面FC1C的法向量将二面角问题转化为向量夹角问题.
| AF |
| EC1 |

练习册系列答案
相关题目
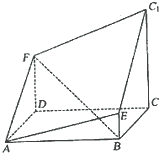
 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1. 已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
 的长方体被截面
的长方体被截面 所截面而得到的,其中
所截面而得到的,其中 ,
, .
. 的长;
的长; 到平面
到平面