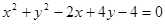题目内容
在斜坐标系xOy中,∠xOy,. |
| e1 |
. |
| e2 |
. |
| OP |
. |
| e1 |
. |
| e2 |
(1)已知P的斜坐标为(
| 2 |
. |
| OP |
(2)在此坐标平面內,以O为原点,半径为1的_的方程是
分析:(1)根据p点的坐标表示出向量
,进而由|
|2=(
e1+e2)2可得答案.
(2)设圆上任意点M的坐标然后表示出
=xe1+ye2,根据|
|=1找出x,y的关系即可.
| OP |
| OP |
| 2 |
(2)设圆上任意点M的坐标然后表示出
| OM |
| OM |
解答:解:(1)∵P点斜坐标为(
,1),
∴
=
e1+e2.∴|
|2=(
e1+e2)2=3+2
e1•e2=5.
∴|
|=
,即|OP|=
.
(2)设圆上动点M的斜坐标为(x,y),则
=xe1+ye2.
∴(xe1+ye2)2=1.∴x2+y2+2xye1•e2=1.∴x2+y2+
xy=1.
故所求方程为x2+y2+
xy=1.
故答案为:(1)
;(2)x2+y2+
xy-1=0
| 2 |
∴
| OP |
| 2 |
| OP |
| 2 |
| 2 |
∴|
| OP |
| 5 |
| 5 |
(2)设圆上动点M的斜坐标为(x,y),则
| OM |
∴(xe1+ye2)2=1.∴x2+y2+2xye1•e2=1.∴x2+y2+
| 2 |
故所求方程为x2+y2+
| 2 |
故答案为:(1)
| 5 |
| 2 |
点评:本题主要考查平面向量的坐标表示和运算,解答的关键是将新定义的斜坐标转化为熟悉的直角坐标进行运算.属中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:
如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的: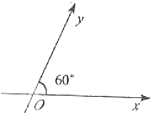 如图,在平在斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系中的斜坐标是这样定义的:若
如图,在平在斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系中的斜坐标是这样定义的:若
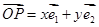 (其中
(其中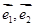 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若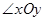 =120°,点M的斜坐标为(1,2),则以点M为圆心,1为半径的圆在斜坐标系xOy中的方程是
( )
=120°,点M的斜坐标为(1,2),则以点M为圆心,1为半径的圆在斜坐标系xOy中的方程是
( )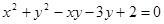 B.
B. 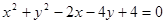
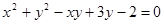 D.
D.