题目内容
已知函数 的定义域为
的定义域为 ,值域为[-5,4];函数
,值域为[-5,4];函数  .
.
(Ⅰ) 求函数g(x)的最小正周期和最大值;
(Ⅱ) 当 , 且g(x) =5时, 求tan x.
, 且g(x) =5时, 求tan x.
 的定义域为
的定义域为 ,值域为[-5,4];函数
,值域为[-5,4];函数  .
.(Ⅰ) 求函数g(x)的最小正周期和最大值;
(Ⅱ) 当
 , 且g(x) =5时, 求tan x.
, 且g(x) =5时, 求tan x.(Ⅰ)当a>0时,T=2p, g(x)max=5;当a<0时,T=p, g(x)max=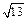
(Ⅱ) tan x=-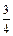
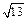
(Ⅱ) tan x=-
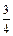
f(x)=a(1-cos2x)-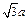 sin2x+b
sin2x+b
=-a(cos2x+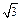 sin2x)+a+b=-2asin(2x+
sin2x)+a+b=-2asin(2x+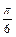 )+a+b . ----------2分
)+a+b . ----------2分
∵x∈ ,∴2x+
,∴2x+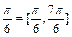 ,sin(2x+
,sin(2x+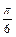 )Î
)Î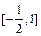 . 显然a=0不合题意.---- -3分
. 显然a=0不合题意.---- -3分
(1) 当a>0时,值域为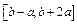 ,即
,即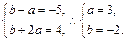 ----------5分
----------5分
(2) 当a<0时,值域为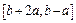 ,即
,即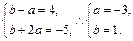 ········ 6分
········ 6分
(Ⅰ) 当a>0时,g(x)=3sinx-4cosx=5sin(x+j1), ∴T=2p, g(x)max=5;
当a<0时,g(x)= -3sinx+2cosx=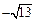 sin(x+j2),
sin(x+j2),
∴ T=p, g(x)max=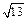 .······················ 8分
.······················ 8分
(Ⅱ)由上可知,
当a>0时, 由g(x)=5sin(x+j1),且tanj1=-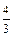 , g(x)max=5,此时x+j1=2kp+
, g(x)max=5,此时x+j1=2kp+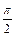 (k∈Z).
(k∈Z).
则x=2kp+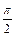 -j1(k∈Z), x∈(0,p),∴tanx=cotj1=-
-j1(k∈Z), x∈(0,p),∴tanx=cotj1=-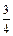 .10分
.10分
当a<0时, g(x)max=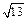 <5,所以不存在符合题意的x. ---------12分
<5,所以不存在符合题意的x. ---------12分
综上,tan x=-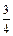 . -------------------13分
. -------------------13分
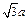 sin2x+b
sin2x+b=-a(cos2x+
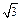 sin2x)+a+b=-2asin(2x+
sin2x)+a+b=-2asin(2x+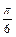 )+a+b . ----------2分
)+a+b . ----------2分∵x∈
 ,∴2x+
,∴2x+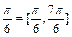 ,sin(2x+
,sin(2x+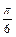 )Î
)Î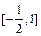 . 显然a=0不合题意.---- -3分
. 显然a=0不合题意.---- -3分(1) 当a>0时,值域为
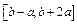 ,即
,即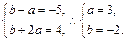 ----------5分
----------5分(2) 当a<0时,值域为
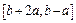 ,即
,即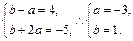 ········ 6分
········ 6分(Ⅰ) 当a>0时,g(x)=3sinx-4cosx=5sin(x+j1), ∴T=2p, g(x)max=5;
当a<0时,g(x)= -3sinx+2cosx=
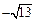 sin(x+j2),
sin(x+j2),∴ T=p, g(x)max=
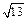 .······················ 8分
.······················ 8分(Ⅱ)由上可知,
当a>0时, 由g(x)=5sin(x+j1),且tanj1=-
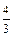 , g(x)max=5,此时x+j1=2kp+
, g(x)max=5,此时x+j1=2kp+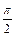 (k∈Z).
(k∈Z).则x=2kp+
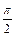 -j1(k∈Z), x∈(0,p),∴tanx=cotj1=-
-j1(k∈Z), x∈(0,p),∴tanx=cotj1=-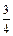 .10分
.10分当a<0时, g(x)max=
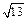 <5,所以不存在符合题意的x. ---------12分
<5,所以不存在符合题意的x. ---------12分综上,tan x=-
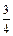 . -------------------13分
. -------------------13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
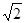 米
米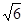 米
米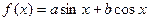 的图象经过点
的图象经过点
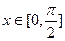 ,求函数
,求函数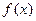 的最大值及此时x的值.
的最大值及此时x的值.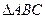 中,
中,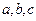 分别为内角
分别为内角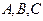 所对的边,且满足
所对的边,且满足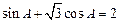 .
.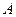 的大小;
的大小;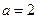 ; ②
; ②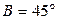 ;③
;③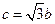 .
.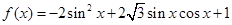
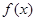 的最小正周期及对称中心;
的最小正周期及对称中心;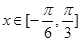 ,求
,求 ,
, , 且
, 且
 的值.(2)求
的值.(2)求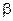 的大小.
的大小.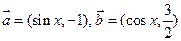 .
.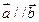 时,求
时,求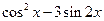 的值;(2)求
的值;(2)求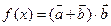 的单调增区间.
的单调增区间.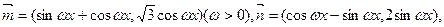 函数
函数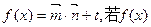 图象上相邻两个对称轴间的距离为
图象上相邻两个对称轴间的距离为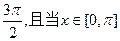 时,函数
时,函数 的最小值为0.
的最小值为0.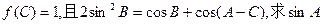 的值.
的值. 中,
中, ,
, ,面积为
,面积为 ,则
,则 