题目内容
(1)若直角三角形两直角边长之和为12,求其周长p的最小值;(2)若三角形有一个内角为
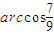 ,周长为定值p,求面积S的最大值;
,周长为定值p,求面积S的最大值;(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)2-c2][c2-(a-b)2]=-c4+2(a2+b2)c2-(a2-b2)2=-[c2-(a2+b2)]2+4a2b2
而-[c2-(a2+b2)]2≤0,a2≤81,b2≤64,则S≤36,但是,其中等号成立的条件是c2=a2+b2,a=9,b=8,于是c2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
【答案】分析:(1)设直角三角形两直角边长为x、12-x,斜边长为y,由勾股定理和二次函数的性质求出y的最小值,即得周长p的
最小值.
(2)根据周长p=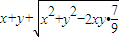 ,利用基本不等式求得
,利用基本不等式求得 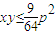 ,再由S=
,再由S= =
=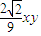 ,求得面积S的最大值.
,求得面积S的最大值.
(3)不正确,由海伦公式化简可得16S2=-[a2-(b2+c2)]2+4b2c2 ,而-[a2-(b2+c2)]2≤0,b2≤64,c2≤16,
则S≤16,故当三角形的边长为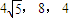 的直角三角形时,其面积取得最大值16.
的直角三角形时,其面积取得最大值16.
另解: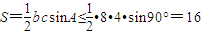 .
.
解答:解:(1)设直角三角形两直角边长为x、12-x,斜边长为y,则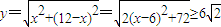 ,
,
∴两直角边长为6时,周长p的最小值为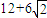 .
.
(2)设三角形中边长为x、y的两边所夹的角为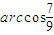 ,则周长p=
,则周长p= ,
,
∴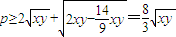 ,即
,即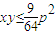 .
.
又S=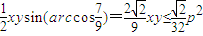 ,∴为
,∴为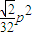 .
.
(3)不正确.16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(b+c)2-a2][a2-(b-c)2]
=-a4+2(b2+c2)a2-(b2-c2)2 =-[a2-(b2+c2)]2+4b2c2
而-[a2-(b2+c2)]2≤0,b2≤64,c2≤16,则S≤16,
其中等号成立的条件是 a2=b2+c2,b=8,c=4,则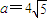 .
.
∴当三角形的边长为 的直角三角形时,其面积取得最大值16.
的直角三角形时,其面积取得最大值16.
( 另解: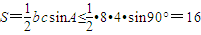 )
)
点评:本题考查基本不等式,反余弦函数的定义,海伦公式的应用,三角形中的几何计算,属于中档题.
最小值.
(2)根据周长p=
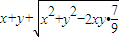 ,利用基本不等式求得
,利用基本不等式求得 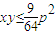 ,再由S=
,再由S= =
=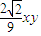 ,求得面积S的最大值.
,求得面积S的最大值.(3)不正确,由海伦公式化简可得16S2=-[a2-(b2+c2)]2+4b2c2 ,而-[a2-(b2+c2)]2≤0,b2≤64,c2≤16,
则S≤16,故当三角形的边长为
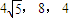 的直角三角形时,其面积取得最大值16.
的直角三角形时,其面积取得最大值16.另解:
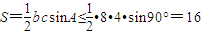 .
.解答:解:(1)设直角三角形两直角边长为x、12-x,斜边长为y,则
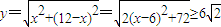 ,
,∴两直角边长为6时,周长p的最小值为
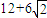 .
.(2)设三角形中边长为x、y的两边所夹的角为
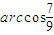 ,则周长p=
,则周长p= ,
,∴
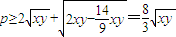 ,即
,即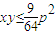 .
.又S=
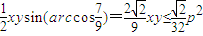 ,∴为
,∴为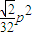 .
.(3)不正确.16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(b+c)2-a2][a2-(b-c)2]
=-a4+2(b2+c2)a2-(b2-c2)2 =-[a2-(b2+c2)]2+4b2c2
而-[a2-(b2+c2)]2≤0,b2≤64,c2≤16,则S≤16,
其中等号成立的条件是 a2=b2+c2,b=8,c=4,则
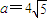 .
.∴当三角形的边长为
 的直角三角形时,其面积取得最大值16.
的直角三角形时,其面积取得最大值16.( 另解:
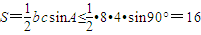 )
)点评:本题考查基本不等式,反余弦函数的定义,海伦公式的应用,三角形中的几何计算,属于中档题.

练习册系列答案
相关题目
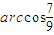 ,周长为定值p,求面积S的最大值;
,周长为定值p,求面积S的最大值;