题目内容
（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
（2）若三角形有一个内角为arccos
，周长为定值p，求面积S的最大值；
（3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
absinC≤
×9×8sinC=36sinC，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时cosC=
，sinC=
，所以，该三角形面积的最大值是
．以上解答是否正确？若不正确，请你给出正确的解答．
（2）若三角形有一个内角为arccos
| 7 |
| 9 |
（3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
| 1 |
| 2 |
| 1 |
| 2 |
| 43 |
| 48 |
| ||
| 48 |
3
| ||
| 4 |
（1）设直角三角形两直角边长分别为x、12-x，斜边长为y，则 y=
=
≥6
，
∴两直角边长都为6时，周长p的最小值为 12+6
．
（2）设三角形中边长为x、y的两边所夹的角为 arccos
，则周长p=x+y+
，
∴p≥2
+
=
，即 xy≤
p2．
又S=
xysin(arccos
)=
xy≤
p2，∴面积S的最大值为
p2．
（3）不正确．16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）=[（b+c）2-a2][a2-（b-c）2]
=-a4+2（b2+c2）a2-（b2-c2）2=-[a2-（b2+c2）]2+4b2c2，
而-[a2-（b2+c2）]2≤0，b2≤64，c2≤16，则S≤16．
其中等号成立的条件是 a2=b2+c2，b=8，c=4，则 a=4
．
∴当三角形的边长a、b、c 分别为 4
，8，4的直角三角形时，其面积取得最大值16．
（ 另S=
bcsinA≤
•8•4•sin90°=16）．
| x2+(12-x)2 |
| 2(x-6)2+72 |
| 2 |
∴两直角边长都为6时，周长p的最小值为 12+6
| 2 |
（2）设三角形中边长为x、y的两边所夹的角为 arccos
| 7 |
| 9 |
x2+y2-2xy•
|
∴p≥2
| xy |
2xy-
|
| 8 |
| 3 |
| xy |
| 9 |
| 64 |
又S=
| 1 |
| 2 |
| 7 |
| 9 |
2
| ||
| 9 |
| ||
| 32 |
| ||
| 32 |
（3）不正确．16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）=[（b+c）2-a2][a2-（b-c）2]
=-a4+2（b2+c2）a2-（b2-c2）2=-[a2-（b2+c2）]2+4b2c2，
而-[a2-（b2+c2）]2≤0，b2≤64，c2≤16，则S≤16．
其中等号成立的条件是 a2=b2+c2，b=8，c=4，则 a=4
| 5 |
∴当三角形的边长a、b、c 分别为 4
| 5 |
（ 另S=
| 1 |
| 2 |
| 1 |
| 2 |
练习册系列答案
相关题目
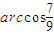，周长为定值p，求面积S的最大值；
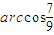，周长为定值p，求面积S的最大值；