题目内容
若函数f(x)=cosx+2|cosx|-m在x∈[0,2π]上仅有两个不同的零点,则实数m的取值范围为________.
(1,3)∪{0}
分析:根据cosx≥0和cosx<0对应的x的范围,去掉绝对值化简函数解析式,再由解析式画出函数的图象,由图象求出m的取值范围.
解答: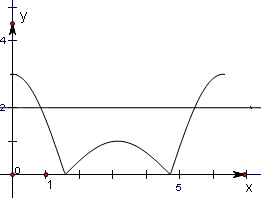 解:由题意知,
解:由题意知,
设g(x)=cosx+2|cosx|,
则g(x)=cosx+2|cosx|=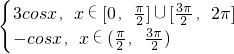 ,
,
在坐标系中画出函数g(x)图象:
由其图象可知当直线y=m,m∈(1,3)∪{0}时,
g(x)=cosx+2|cosx|,x∈[0,2π]的图象与直线y=m有且仅有两个不同的交点.
故答案为:(1,3)∪{0}
点评:本题的考点是余弦函数的图象应用,即根据x的范围化简函数解析式,根据余弦函数的图象画出原函数的图象,再由图象求解,考查了数形结合思想和作图能力.
分析:根据cosx≥0和cosx<0对应的x的范围,去掉绝对值化简函数解析式,再由解析式画出函数的图象,由图象求出m的取值范围.
解答:
 解:由题意知,
解:由题意知,设g(x)=cosx+2|cosx|,
则g(x)=cosx+2|cosx|=
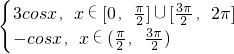 ,
,在坐标系中画出函数g(x)图象:
由其图象可知当直线y=m,m∈(1,3)∪{0}时,
g(x)=cosx+2|cosx|,x∈[0,2π]的图象与直线y=m有且仅有两个不同的交点.
故答案为:(1,3)∪{0}
点评:本题的考点是余弦函数的图象应用,即根据x的范围化简函数解析式,根据余弦函数的图象画出原函数的图象,再由图象求解,考查了数形结合思想和作图能力.

练习册系列答案
相关题目