题目内容
点O是 ABC所在平面内一定点,动点P满足
ABC所在平面内一定点,动点P满足 ,则动点P的轨迹一定通过三角形ABC的( )
,则动点P的轨迹一定通过三角形ABC的( )
| A.重心 | B.垂心 | C.外心 | D.内心 |
A
解析试题分析:出如图的三角形AD⊥BC,可以得出| 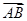 |sinB=|
|sinB=| 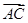 |sinC=AD,由此对已知条件变形即可得出结论
|sinC=AD,由此对已知条件变形即可得出结论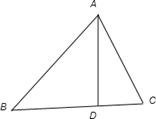
解:作出如图的图形AD⊥BC,由于| 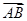 |sinB=|
|sinB=| 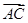 |sinC=AD∴
|sinC=AD∴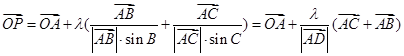
由加法法则知,P在三角形的中线上,故动点P的轨迹一定通过△ABC的重心,故选A
考点:三角形的五心
点评:本题考点是三角形的五心,考查了五心中重心的几何特征以及向量的加法与数乘运算,解答本题的关键是理解向量加法的几何意义,从而确定点的几何位置.

练习册系列答案
相关题目
在 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,
的中点, ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
设 ,向量
,向量 ,b=(3,—2),且
,b=(3,—2),且 则|a-b|=( )
则|a-b|=( )
| A.5 | B. | C.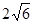 | D.6 |
空间四边形 中,
中,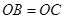 ,
, ,则
,则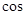 <
<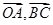 >的值是( )
>的值是( )
A. | B. | C.- | D. |
已知O是 内部一点,
内部一点, 则
则 的面积为( )
的面积为( )
A. | B. | C. | D. |
已知向量 ,
,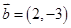 ,若向量
,若向量 满足
满足 ,
, ,则
,则 ="(" )
="(" )
A. | B.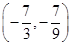 | C. | D. |
已知向量 且
且 ,则
,则 等于
等于
A. | B.- | C. | D.- |
 是
是 的重心,过
的重心,过 ,
, 两边分别交于
两边分别交于 ,
, 两点,且
两点,且 ,
, ,则
,则 的值为( )
的值为( )


 ,点
,点 为
为 所表示的平面区域内任意一点,
所表示的平面区域内任意一点, ,
, 为坐标原点,
为坐标原点, 为
为 的最小值,则
的最小值,则


