题目内容
 如图,A、B为半椭圆
如图,A、B为半椭圆| y2 | 4 |
(1)求△ABF的外接圆圆心;
(2)过焦点F的直线L与曲线C交于P、Q两点,若|PQ|=2,求所有满足条件的直线L;
(3)对于一般的封闭曲线,曲线上任意两点距离的最大值称为该曲线的“直径”.如圆的“直径”就是通常的直径,椭圆的“直径”就是长轴的长.求该曲线C的“直径”.
分析:(1)先判断△ABF的形状,为边长为2的等边三角形,再利用等边三角形的性质求圆心坐标即可.
(2)先讨论P,Q点的位置,只能两点都在椭圆上,设出PQ方程,与椭圆方程联立,解x1+x2,x1x2,用弦长公式求出
|PQ|的长,用含k的式子表示,根据|PQ|=2,就可求出k值.
(3)先设曲线C上两动点的坐标,代入两点间距离公式,再根据利用放缩法,以及椭圆上点的范围即可求出两点连线的范围,求出“直径”长.
(2)先讨论P,Q点的位置,只能两点都在椭圆上,设出PQ方程,与椭圆方程联立,解x1+x2,x1x2,用弦长公式求出
|PQ|的长,用含k的式子表示,根据|PQ|=2,就可求出k值.
(3)先设曲线C上两动点的坐标,代入两点间距离公式,再根据利用放缩法,以及椭圆上点的范围即可求出两点连线的范围,求出“直径”长.
解答:解:(1)A(-1,0),B(1,0),F(0,
),故△ABF是边长为2的等边三角形,外接圆半径R=
,故圆心为(0,
)
(2)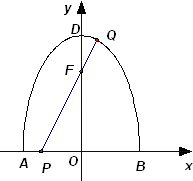 记椭圆的上顶点为D(0,2),若直线L与曲线C的两交点一个在椭圆上,一个在线段AB上,
记椭圆的上顶点为D(0,2),若直线L与曲线C的两交点一个在椭圆上,一个在线段AB上,
如图.因为FQ≥FD,FP≥FO,即此时|PQ|≥|OD|=2,
故只有直线x=0符合题意;
设点P、Q都在椭圆上,P(x1,y1),Q(x2,y2),
直线L:y=kx+
,则
⇒(k2+4)x2+2
kx-1=0
⇒(x1-x2)2=
所以|PQ|=
| x1-x2|=
=2,得k=±
经检验,满足题意的直线L有三条,分别为x=0,y=
x+
,y=-
x+
(3)设曲线C上两动点G(x,y),H(x0,y0),
显然G、H至少有一点在椭圆上时GH才能取得最大,不妨设y≥y0≥0,则
|GH|2=(x-x0)2+(y-y0)2≤(x-x0)2+y2=(x-x0)2+4(1-x2)
=-3x2-2x0x+x02+4=-3(x+
)2+
+4≤
+4≤
+4=
等号成立时G(
,
),H(-1,0)或G(-
,
),H(1,0),故曲线C的直径为
.
| 3 |
2
| ||
| 3 |
| ||
| 3 |
(2)
 记椭圆的上顶点为D(0,2),若直线L与曲线C的两交点一个在椭圆上,一个在线段AB上,
记椭圆的上顶点为D(0,2),若直线L与曲线C的两交点一个在椭圆上,一个在线段AB上,如图.因为FQ≥FD,FP≥FO,即此时|PQ|≥|OD|=2,
故只有直线x=0符合题意;
设点P、Q都在椭圆上,P(x1,y1),Q(x2,y2),
直线L:y=kx+
| 3 |
|
| 3 |
|
| 16(k2+1) |
| (k2+4)2 |
所以|PQ|=
| k2+1 |
| 4(k2+1) |
| (k2+4)2 |
| 2 |
经检验,满足题意的直线L有三条,分别为x=0,y=
| 2 |
| 3 |
| 2 |
| 3 |
(3)设曲线C上两动点G(x,y),H(x0,y0),
显然G、H至少有一点在椭圆上时GH才能取得最大,不妨设y≥y0≥0,则
|GH|2=(x-x0)2+(y-y0)2≤(x-x0)2+y2=(x-x0)2+4(1-x2)
=-3x2-2x0x+x02+4=-3(x+
| x0 |
| 3 |
| 4x02 |
| 3 |
| 4x02 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
等号成立时G(
4
| ||
| 3 |
| 1 |
| 3 |
4
| ||
| 3 |
| 1 |
| 3 |
4
| ||
| 3 |
点评:本题主要考查了直线与圆锥曲线相交时弦长公式的应用,韦达定理的应用,两点间距离公式的应用.

练习册系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: 如图,椭圆C:
如图,椭圆C: 请阅读以下材料,然后解决问题:
请阅读以下材料,然后解决问题: (2013•济宁一模)如图,已知半椭圆C1:
(2013•济宁一模)如图,已知半椭圆C1: