题目内容
已知直线l过点P(0,1),且l夹在两直线l1:x-3y+10=0与l2:2x+y-8=0之间的线段恰好被P点平分,则直线l的方程为 .
【答案】分析:根据直线l1、l2的方程,设直线l与直线l1、l2的交点分别为A(3a-10,a)和B(b,8-2b),由线段中点公式建立关于a、b的方程组,解出a=2且b=4,从而得到A、B的坐标,最后用直线方程的两点式列式,化简整理即得直线l的方程.
解答:解:设直线l与直线l1相交于点A(3a-10,a),直线l与l2相交于点B(b,8-2b),
∵线段AB的中点为P(0,1)
∴ ,解之得
,解之得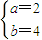
由此可得A(-4,2),B(4,0)
∴直线l的方程为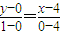 ,化简得x+4y-4=0
,化简得x+4y-4=0
故答案为:x+4y-4=0
点评:本题给出一条直线被两条相交直线所截,在已知截得线段中点的情况下求直线的方程.着重考查了直线的基本量和基本形式、中点坐标公式等知识,属于基础题.
解答:解:设直线l与直线l1相交于点A(3a-10,a),直线l与l2相交于点B(b,8-2b),
∵线段AB的中点为P(0,1)
∴
 ,解之得
,解之得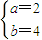
由此可得A(-4,2),B(4,0)
∴直线l的方程为
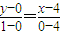 ,化简得x+4y-4=0
,化简得x+4y-4=0故答案为:x+4y-4=0
点评:本题给出一条直线被两条相交直线所截,在已知截得线段中点的情况下求直线的方程.着重考查了直线的基本量和基本形式、中点坐标公式等知识,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
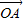 +
+ 与
与 共线?若存在,求出k的值;若不存在,请说明理由.
共线?若存在,求出k的值;若不存在,请说明理由.