题目内容
已知直线l过点P(0,2),斜率为k,圆Q:x2+y2-12x+32=0,若直线l和圆Q交于两个不同的点A,B,问是否存在常数k,使得
+
与
共线?若存在,求出k的值;若不存在,请说明理由.
| OA |
| OB |
| PQ |
分析:设直线l的方程为y=kx+2,将l的方程和圆方程联解,消去y得到关于x的一元二次方程,利用根与系数的关系及
+
与
共线,建立关于k的等式解出k=-
.再由根的判别式大于零可得-
<k<0,因此不存在常数k,使得
+
与
共线.
| OA |
| OB |
| PQ |
| 3 |
| 4 |
| 3 |
| 4 |
| OA |
| OB |
| PQ |
解答:解:设直线l的方程为y=kx+2,
由
消y,可得(1+k2)x2+4(k-3)x+36=0,
∵直线l和圆相交,
∴△=[4(k-3)]2-4×36×(1+k2)>0,解得-
<k<0.
设A(x1,y1)、B(x2,y2),
由根与系数的关系,可得x1+x2=-
,x1x2=
.…①
∴y1+y2=kx1+2+kx2+2=k(x1+x2)+4,…②
∵
+
=(x1+x2,y1+y2),
=(6,-2).
若
+
与
共线,则-2×(x1+x2)=6×(y1+y2),即(1+3k)(x1+x2)+12=0,
代入①②,可得(1+3k)[-
]+12=0,解得k=-
.
又∵-
<k<0,
∴不存在常数k,使得
+
与
共线.
由
|
∵直线l和圆相交,
∴△=[4(k-3)]2-4×36×(1+k2)>0,解得-
| 3 |
| 4 |
设A(x1,y1)、B(x2,y2),
由根与系数的关系,可得x1+x2=-
| 4(k+3) |
| 1+k2 |
| 36 |
| 1+k2 |
∴y1+y2=kx1+2+kx2+2=k(x1+x2)+4,…②
∵
| OA |
| OB |
| PQ |
若
| OA |
| OB |
| PQ |
代入①②,可得(1+3k)[-
| 4(k+3) |
| 1+k2 |
| 3 |
| 4 |
又∵-
| 3 |
| 4 |
∴不存在常数k,使得
| OA |
| OB |
| PQ |
点评:本题给出经过定点的直线与圆的方程,探究使
+
与
共线的直线是否存在.着重考查了向量共线的条件、直线的方程、圆的方程和直线与圆的位置关系等知识,属于中档题.
| OA |
| OB |
| PQ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
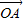 +
+ 与
与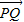 共线?若存在,求出k的值;若不存在,请说明理由.
共线?若存在,求出k的值;若不存在,请说明理由.