题目内容
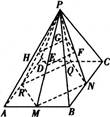
如图所示，已知P 是平行四边形ABCD 所在平面外一点，连结PA 、PB 、PC 、PD ，点E 、F 、G 、H 分别为△PAB 、△PBC 、△PCD 、 △PDA 的重心，求证：E 、F 、G 、H 四点共面
证明：分别延长P 、PF 、PG 、PH 交对边于M 、N 、Q 、R ．
∵E 、F 、G 、H 分别是所在三角形的重心，
∴M 、N 、Q 、R 为所在边的中点，
顺次连结MNQR 所得四边形为平行四边形，
且有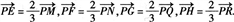
∵MNQR为平行四边形，
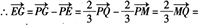
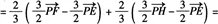
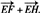
∴由共面向量定理得E、F、G、H四点共面.
∵E 、F 、G 、H 分别是所在三角形的重心，
∴M 、N 、Q 、R 为所在边的中点，
顺次连结MNQR 所得四边形为平行四边形，
且有
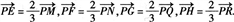
∵MNQR为平行四边形，
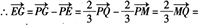
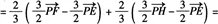
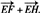
∴由共面向量定理得E、F、G、H四点共面.
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
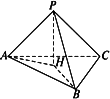
如图所示，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点，平面PAD∩平面PBC=l．
如图所示，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点，平面PAD∩平面PBC=l．