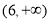题目内容
一次函数
是
上的增函数，
,已知
.
（1）求；
（2）若
在
单调递增，求实数
的取值范围；
（3）当
时，
有最大值
，求实数
的值.
(1) 
;(2) 
的取值范围为
;(3) 
或
.
【解析】
试题分析：（1）利用待定系数法设
，
，
，解得
或
（不合题意舍去），
∴；
（2）由（1）有
，根据二次函数的性质，当
在
单调递增，则对称轴
，解得
；
（3）分情况讨论，考虑对称轴的位置，利用单调性求最值，①当时，即时
，解得，符合题意；②当
时，即
时
，解得，符合题意；由①②可得或.
试题解析：（1）∵
是
上的增函数，∴设 1分
∴， 3分
解得或（不合题意舍去） 5分
∴ 6分
（2）
7分
对称轴
，根据题意可得， 8分
解得
∴的取值范围为 9分
（3）①当时，即时
，解得，符合题意； 11分
②当时，即时
，解得，符合题意； 13分
由①②可得或 14分
考点：本题考查函数的解析式求法，二次函数的单调性和最值性，分类讨论思想.
练习册系列答案
相关题目
