题目内容
在面积为9的三角形ABC中,tanA=-![]() ,且
,且![]()
(1)建立适合的坐标系,求以AB、AC所在直线为渐近线且过点D的双曲线的方程.
(2)过D分别作AB、AC所在直线的垂线DE、DF(E、F为垂足),求![]() 的值.
的值.
解:(1)以点A为坐标原点,∠CAB的平分线所在的直线为![]() 轴,
轴,
建立平面直角坐标系,设∠CA![]() =
=![]() .
.
∵tanA=![]() ,∴tan
,∴tan![]() =2,
=2,
所以AC的方程为![]() ,AB方程为
,AB方程为![]() .
.
双曲线方程可设为![]() .
.
设B(![]() ,一2
,一2![]() )、C(
)、C(![]() ,2
,2![]() ),由
),由![]()
得D(![]() ),
),
∴4(![]()
即![]() ①
①
由tanA=-![]() 可得sinA=
可得sinA=![]() .
.
又∵|AB|一![]() ,|AC|=
,|AC|=![]() (
(![]() >0)
>0)
∴S△ABC=![]() |AB||AC|sinA
|AB||AC|sinA
=![]() ×5
×5![]() ×
×![]()
=2![]() =9,
=9,
即![]() =
=![]() ,代入式①得
,代入式①得![]() =16.
=16.
双曲线的方程为![]() .
.
(2)由题设可知![]() ,
,
∴cos![]() .
.
设D为(![]() ,
,![]() ),则
),则![]() .
.
则点D到AB、AC所在直线距离为
![]() 、
、![]()
而![]()
=![]()
=![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 在点
在点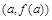 处的切线与两条坐标轴围成的三角形的面积为54,则
处的切线与两条坐标轴围成的三角形的面积为54,则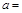 ( )
( )