题目内容
【题目】设抛物线y2=2px(p>0)的焦点为F,其准线与x轴的交点为Q,过Q点的直线l交抛物线于A,B两点.
(1)若直线l的斜率为 ![]() ,求证:
,求证: ![]() ;
;
(2)设直线FA,FB的斜率分别为k1 , k2 , 求k1+k2的值.
【答案】
(1)证明:由题意可得 ![]() ,
,
联立 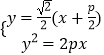 ,得
,得 ![]() .
.
设A(x1,y1),B(x2,y2),
![]() .
.
则 ![]() .
.
∴ ![]()
(2)解:设直线 ![]() ,与抛物线联立得y2﹣2pky+p2=0.
,与抛物线联立得y2﹣2pky+p2=0.
∴ ![]() .
.
则 ![]()
【解析】(1)由点斜式写出直线l的方程,和抛物线方程联立后化为关于x的一元二次方程,利用根与系数关系求出A,B两点的横坐标的和与积,写出向量 ![]() 的坐标,展开数量积后代入根与系数关系得答案;(2)设直线l的方程为
的坐标,展开数量积后代入根与系数关系得答案;(2)设直线l的方程为 ![]() ,和抛物线方程联立后化为关于y的一元二次方程,写出根与系数关系,由两点式求出斜率后作和化简,代入根与系数关系即可得到答案.
,和抛物线方程联立后化为关于y的一元二次方程,写出根与系数关系,由两点式求出斜率后作和化简,代入根与系数关系即可得到答案.

练习册系列答案
相关题目