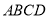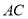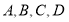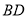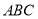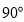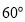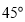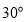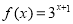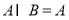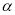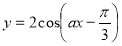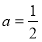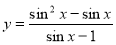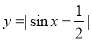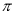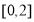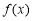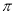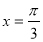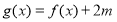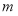题目内容
已知函数 .
.
(1)若 的定义域和值域均是
的定义域和值域均是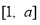 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,都有
,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,且对任意的
,且对任意的 ,都存在
,都存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)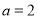 ;(2)
;(2)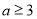 ;(3)
;(3)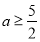 .
.
【解析】
试题分析:(1)先利用二次函数的性质确定函数 的单调递减区间为
的单调递减区间为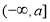 ,故
,故 在
在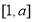 单调递减,然后由定义域与值域列出等式关系,从而求解即可;(2)由(1)可知
单调递减,然后由定义域与值域列出等式关系,从而求解即可;(2)由(1)可知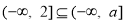 ,初步确定
,初步确定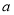 的取值范围
的取值范围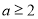 ,然后确定
,然后确定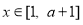 时函数
时函数 的最大值
的最大值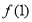 ,从中求解不等式组
,从中求解不等式组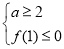 即可;(3)将“对任意的
即可;(3)将“对任意的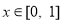 ,都存在
,都存在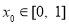 ,使得
,使得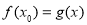 成立”转化为
成立”转化为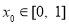 时,
时,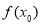 的值域包含了
的值域包含了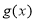 在
在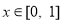 的值域,然后进行分别求
的值域,然后进行分别求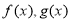 在
在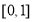 的值域,从集合间的包含关系即可求出
的值域,从集合间的包含关系即可求出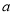 的取值范围.
的取值范围.
试题解析:(1)∵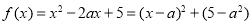
∴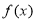 在
在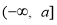 上单调递减,又
上单调递减,又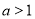 ,∴
,∴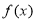 在
在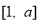 上单调递减,
上单调递减,
∴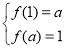 ,∴
,∴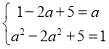 ,∴
,∴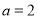 4分
4分
(2)∵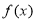 在区间
在区间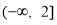 上是减函数,∴
上是减函数,∴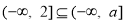 ,∴
,∴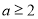
∴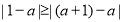 ,
,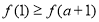
∴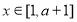 时,
时,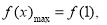
又∵对任意的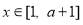 ,都有
,都有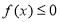 ,
,
∴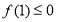 ,即
,即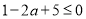 ,也就是
,也就是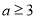
综上可知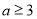 8分
8分
(3)∵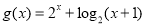 在
在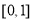 上递增,
上递增,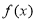 在
在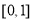 上递减,
上递减,
当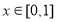 时,
时,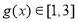 ,
,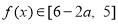
∵对任意的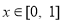 ,都存在
,都存在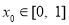 ,使得
,使得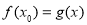 成立
成立
∴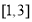
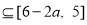
∴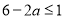 ,所以
,所以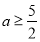 13分
13分
考点:1.二次函数图像与性质;2.函数的单调性;3.函数与方程的问题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目