题目内容
已知函数f(x)=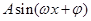 (其中A>0,
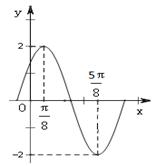
(其中A>0,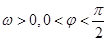 )的图象如图所示。
)的图象如图所示。
(1)求A,w及j的值;
(2)若tana=2,求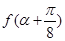 的值.
的值.
【答案】
解:(Ⅰ)由图知A=2,
T=2(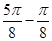 )=p,
)=p,
∴w=2, ∴f(x)=2sin(2x+j)
又∵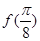 =2sin(
=2sin(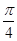 +j)=2,
+j)=2,
∴sin(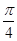 +j)=1, ∴
+j)=1, ∴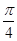 +j=
+j=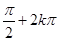 ,j=
,j=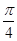 +
+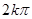 ,(kÎZ)
,(kÎZ)
∵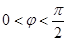 ,∴j=
,∴j=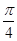 由(Ⅰ)知:f(x)=2sin(2x+
由(Ⅰ)知:f(x)=2sin(2x+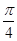 ),
),
∴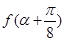 =2sin(2a+
=2sin(2a+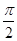 )=2cos2a=4cos2a-2
)=2cos2a=4cos2a-2
∵tana=2, ∴sina=2cosa, 又∵sin2a+cos2a=1, ∴cos2a=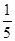 ,
,
∴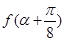 =
=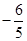
【解析】略

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|