题目内容
请选做一题,都做时按先做的题判分,都做不加分.(1)已知向量
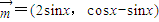 ,
,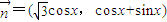 ,函数
,函数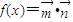 .
.①求函数f(x)的最小正周期和值域;
②在△ABC中,角A、B、C所对的边分别是a、b、c,若
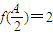 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.(2)已知锐角
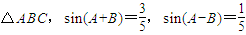 .
.①求证:tanA=2tanB;
②设AB=3,求AB边上的高CD的长.
【答案】分析:(1)①用向量的数量积将函数f(x)的解析式表示出来后化简成y=Asin(ωx+θ)可得答案.
②将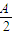 代入函数f(x)可求出A的值,再由余弦定理可得到b=c,从而得到答案.
代入函数f(x)可求出A的值,再由余弦定理可得到b=c,从而得到答案.
(2)①根据两角和与差的正弦公式展开,可得sinAcosB=2cosAsinB,进而得到答案.
②根据正切函数的两角和公式,得出tanA与tanB的关系,再通过①中tanA=2tanB求出tanA和tanB的值.再通过AB=AD+BD= +
+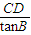 进而求出CD的值.
进而求出CD的值.
解答:解:(1)①f(x)=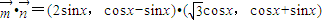
=2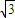 sinxcosx+cos2x-sin2x=
sinxcosx+cos2x-sin2x=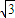 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+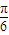 )
)
T=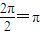 ,值域为[-2,2].
,值域为[-2,2].
②∵f(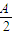 )=2sin(A+
)=2sin(A+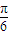 )=2∴A=
)=2∴A=
∵a2=bc
∴cosA=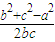 =
=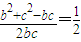 ∴b=c
∴b=c
∴△ABC为等边三角形.
(2)①由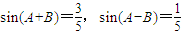 展开可整理得:
展开可整理得:
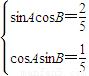
∴sinAcosB=2cosAsinB
∴tanA=2tanB
②∵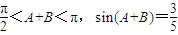 ,
,
∵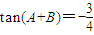 ,即
,即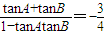 ,
,
又∵tanA=2tanB,∴2tan2B-4tan2B-1=0.
∴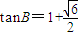 或
或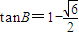 (舍),
(舍),
∴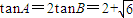 ,
,
∴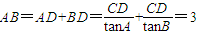 ,
,
∴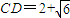 .
.
点评:本题主要考查了三角函数中的两角和公式的运用.此类题常综合三角函数性质、诱导公式、向量等问题.
②将
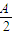 代入函数f(x)可求出A的值,再由余弦定理可得到b=c,从而得到答案.
代入函数f(x)可求出A的值,再由余弦定理可得到b=c,从而得到答案.(2)①根据两角和与差的正弦公式展开,可得sinAcosB=2cosAsinB,进而得到答案.
②根据正切函数的两角和公式,得出tanA与tanB的关系,再通过①中tanA=2tanB求出tanA和tanB的值.再通过AB=AD+BD=
 +
+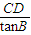 进而求出CD的值.
进而求出CD的值.解答:解:(1)①f(x)=
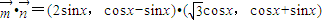
=2
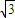 sinxcosx+cos2x-sin2x=
sinxcosx+cos2x-sin2x=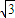 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+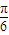 )
)T=
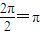 ,值域为[-2,2].
,值域为[-2,2].②∵f(
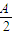 )=2sin(A+
)=2sin(A+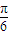 )=2∴A=
)=2∴A=
∵a2=bc
∴cosA=
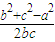 =
=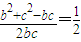 ∴b=c
∴b=c∴△ABC为等边三角形.
(2)①由
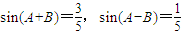 展开可整理得:
展开可整理得: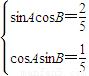
∴sinAcosB=2cosAsinB
∴tanA=2tanB
②∵
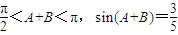 ,
,∵
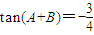 ,即
,即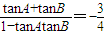 ,
,又∵tanA=2tanB,∴2tan2B-4tan2B-1=0.
∴
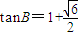 或
或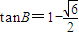 (舍),
(舍),∴
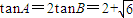 ,
,∴
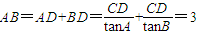 ,
,∴
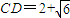 .
.点评:本题主要考查了三角函数中的两角和公式的运用.此类题常综合三角函数性质、诱导公式、向量等问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


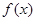 的最小正周期和值域;
的最小正周期和值域; 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状. .
. ;
; ,求AB边上的高CD的长.
,求AB边上的高CD的长.

 的最小正周期和值域;
的最小正周期和值域; 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状. .
. ;
; ,求AB边上的高CD的长.
,求AB边上的高CD的长.