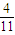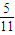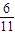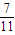题目内容
已知空间4个球,它们的半径分别为2,2,3,3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
分析:设半径为3的两个球的球心分别为A、B,半径为2的两个球的球心分别为C、D,与它们都相切的小球球心为O,半径为r.得如图的四棱锥D-ABCD,其中AB=6,CD=4,AD=AC=BD=BC=5,连接OA、OB、OC、OD,取AB、CD中点F、G,连接OF、OG.可证出FG是异面直线AB、CD的公垂线段且F、O、G三点共线,算出FG=2
,利用OF+OG=FG列出关于r的方程,解之即可得到r的值,即得小球的半径.
| 3 |
解答:解:设半径为3的两个球的球心分别为A、B,半径为2的两个球的球心分别为C、D,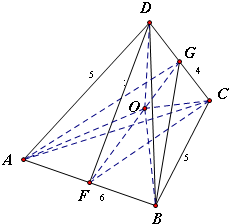
与它们都相切的小球球心为O,半径为r
如图,连接AB、BC、CD、DA、AC、BD,得四棱锥D-ABCD
得AB=6,CD=4,AD=AC=BD=BC=5
连接OA、OB、OC、OD,取AB、CD中点F、G,连接OF、OG
∵等腰△ABC中,CA=CB=5,AF=BF=3
∴CF=
=4,同理可得DF=4
由此可得△CDF中,DF=CF,结合CG=DG,
连接FG,得FG是等腰△CDF底边中线,所以FG⊥CD
同理可得FG⊥AB,所以FG是异面直线AB、CD的公垂线段,
∵OA=OB=3+r,OD=OC=2+r,F、G分别是AB、CD的中点
∴点O在线段FG上,即F、O、G三点共线
∵Rt△AOF中,AF=3,OA=3+r,∴OF=
=
同理可得:OG=
,
∵Rt△CFG中,FG=
=2
∴OF+OG=FG,即
+
=2
,解之得r=
(舍负)
故选:C

与它们都相切的小球球心为O,半径为r
如图,连接AB、BC、CD、DA、AC、BD,得四棱锥D-ABCD
得AB=6,CD=4,AD=AC=BD=BC=5
连接OA、OB、OC、OD,取AB、CD中点F、G,连接OF、OG
∵等腰△ABC中,CA=CB=5,AF=BF=3
∴CF=
| 52-32 |
由此可得△CDF中,DF=CF,结合CG=DG,
连接FG,得FG是等腰△CDF底边中线,所以FG⊥CD
同理可得FG⊥AB,所以FG是异面直线AB、CD的公垂线段,
∵OA=OB=3+r,OD=OC=2+r,F、G分别是AB、CD的中点
∴点O在线段FG上,即F、O、G三点共线
∵Rt△AOF中,AF=3,OA=3+r,∴OF=
| OA2-AF2 |
| (r+3)2-9 |
同理可得:OG=
| (r+2)2-4 |
∵Rt△CFG中,FG=
| CF2-CG2 |
| 3 |
∴OF+OG=FG,即
| (r+3)2-9 |
| (r+2)2-4 |
| 3 |
| 6 |
| 11 |
故选:C
点评:本题给出一个小球与另外四个球都相切,在已知四个大球半径的情况下求小球半径,着重考查了空间直线垂直的判定和球的外切等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
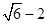 B.
B.
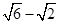 C.
C.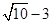 D.
D. 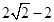
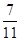 B.
B.
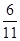 C.
C.
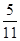 D.
D.

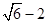 B.
B.
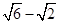 C.
C.
 D.
D.