题目内容
18.已知an=$\left\{\begin{array}{l}{\frac{{3}^{n}-{2}^{n}}{{3}^{n}+{2}^{n}},n≤2014}\\{\frac{{2}^{n}-{3}^{n}}{{2}^{n}+{3}^{n}},n≥2015}\end{array}\right.$,则$\underset{lim}{n→∞}$an=-1.分析 分析知$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$$\frac{2^n-3^n}{2^n+3^n}$=$\underset{lim}{n→∞}$$\frac{(\frac{2}{3})^n-1}{(\frac{2}{3})^n+1}$.
解答 解:当n→∞时,只需考虑an=$\frac{2^n-3^n}{2^n+3^n}$(n≥2015),
则$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$$\frac{2^n-3^n}{2^n+3^n}$=$\underset{lim}{n→∞}$$\frac{(\frac{2}{3})^n-1}{(\frac{2}{3})^n+1}$,
其中,$\underset{lim}{n→∞}$$(\frac{2}{3})^n$=0,
所以,$\underset{lim}{n→∞}$$\frac{(\frac{2}{3})^n-1}{(\frac{2}{3})^n+1}$=$\frac{0-1}{0+1}$=-1,
故填:-1.
点评 本题主要考查了极限及其运算,对于分段数列,其极限只需考虑n→∞时对应的分段,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.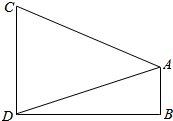 如图,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为( )
如图,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为( )
 如图,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为( )
如图,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
8.已知全集U=R,集合A={1,2,3,4,5},B={x∈R|x>2},下图中阴影部分所表示的集合为( )
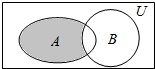

| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
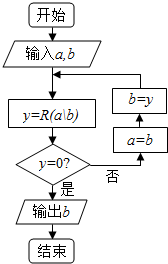 设a,b∈N*,记R(a\b)为a除以b所得的余数,执行如图所示的程序框图,若输入a=243,b=45,则输出的值等于( )
设a,b∈N*,记R(a\b)为a除以b所得的余数,执行如图所示的程序框图,若输入a=243,b=45,则输出的值等于( )