题目内容
过抛物线焦点F的直线与抛物线交于A、B两点,若A、B在抛物线准线上的射影为 、
、 ,则∠
,则∠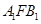 =
=
A. B.
B. 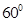 C.
C. 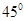 D.
D. 
A
解析考点:抛物线的简单性质.
分析:由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
解:如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK. 由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
故选A。

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知抛物线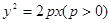 的焦点为
的焦点为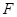 ,
,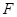 关于原点的对称点为
关于原点的对称点为 过
过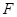 作
作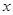 轴的垂线交抛物线于
轴的垂线交抛物线于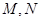 两点.有下列四个命题:①
两点.有下列四个命题:①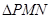 必为直角三角形;②
必为直角三角形;②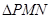 不一定为直角三角形;③直线
不一定为直角三角形;③直线 必与抛物线相切;④直线
必与抛物线相切;④直线 不一定与抛物线相切.其中正确的命题是
不一定与抛物线相切.其中正确的命题是
| A.①③ | B.①④ | C.②③ | D.②④ |
若焦点在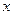 轴上的椭圆
轴上的椭圆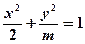 的离心率为
的离心率为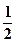 ,则m=( )
,则m=( )
A.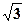 | B.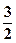 | C.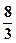 | D.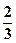 |
已知点A为双曲线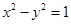 的左顶点,点B和点C在双曲线的右支上,
的左顶点,点B和点C在双曲线的右支上,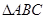 是等边三角形,则
是等边三角形,则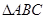 的面积是 ( )
的面积是 ( )
A.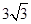 | B.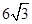 | C.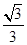 | D. |
如果双曲线的半实轴长为2,焦距为6,那么该双曲线的离心率是 ( )
A.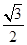 | B.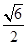 | C.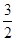 | D.2 |
已知P是椭圆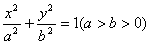 上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
| A.a2 | B.b2 | C.c2 | D.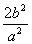 |
已知抛物线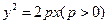 的焦点为
的焦点为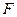 ,点
,点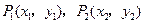 ,
,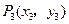 在抛物线上,且
在抛物线上,且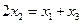 ,则有( )
,则有( )
A. | B.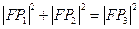 |
C.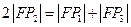 | D.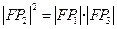 |
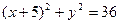 ,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q,则点Q(x,y)所满足的轨迹方程为( ▲ )
,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q,则点Q(x,y)所满足的轨迹方程为( ▲ )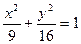


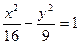
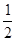 B.x=
B.x=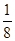 D.y=-
D.y=-