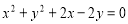题目内容
在某次测验中,有6位同学的平均成绩为75分.用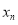 表示编号为
表示编号为 (
( )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(1)s=7;(2)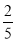
【解析】
试题分析:(1)根据平均数公式写出这组数据的平均数表示式,在表示式中有一个未知量,根据解方程的思想得到结果,求出这组数据的方差,再进一步做出标准差.
(2)本题是一个古典概型,试验发生包含的事件是从5位同学中选2个,共有C52种结果,满足条件的事件是恰有一位成绩在区间(68,75)中,共有C41种结果,根据概率公式得到结果.
试题解析:【解析】
(1)∵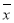 =75,
=75,
∴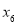 =6×75-70-76-72-70-72=90, 2分
=6×75-70-76-72-70-72=90, 2分
s2=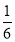 (52+12+32+52+32+152)=49,
(52+12+32+52+32+152)=49,
∴s=7. 4分
(2)从5位同学中随机选取2位同学,共有如下10种不同的取法:
{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5}. 8分
选出的2位同学中,恰有1位同学的成绩位于(68,75)的取法共有如下4种:
{1,2},{2,3},{2,4},{2,5}, 10分
故所求概率为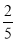 . 12分
. 12分
考点:(1)数字特征;(2)古典概型.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目